Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

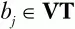
U и С – произвольные нетерминальные символы

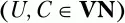
а х и у – произвольные цепочки символов, возможно пустые

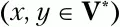
Фактически производится поиск таких правил, в которых в правой части символы а iи Ъ jстоят рядом или же между ними есть не более одного нетерминального символа (причем символ а iобязательно стоит слева от Ь j).

3. Для всех символов Ь j, найденных на шаге 2, выполняем следующее: ставим знак «=.» («составляет основу») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом а i, и столбца, помеченного символом b j.

4. Во всем множестве правил Р ищем правила вида С → xa iU jy, где а i– текущий терминальный символ, U jи С– произвольные нетерминальные символы (U j,

а х и у – произвольные цепочки символов, возможно пустые

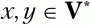
Фактически ищем правила, в которых в правой части символ а iстоит слева от нетерминального символа U j.

5. Для всех символов U j, найденных на шаге 4, берем множество символов L t(U j). Для всех терминальных символов c k, входящих в это множество, выполняем следующее: ставим знак «<.» («предшествует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом a i, и столбца, помеченного символом с k.

6. Во всем множестве правил Р ищем правила вида С → xU ja iy, где a i– текущий терминальный символ, U jи С – произвольные нетерминальные символы

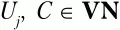
а x и y – произвольные цепочки символов, возможно пустые

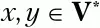
Фактически ищем правила, в которых в правой части символ а стоит справа от нетерминального символа U j.

7. Для всех символов U j, найденных на шаге 6, берем множество символов R t(U j). Для всех терминальных символов c k, входящих в это множество, выполняем следующее: ставим знак «.>» («следует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом с k, и столбца, помеченного символом а i.

8. Если рассмотрены все терминальные символы из множества VT, то переходим к шагу 9, иначе – берем очередной символ

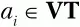
из множества VT, i:= i + 1, делаем его текущим терминальным символом и возвращаемся к шагу 2.

9. Берем множество L t(S) для целевого символа грамматики S. Для всех терминальных символов c k, входящих в это множество, выполняем следующее: ставим знак «<.» («предшествует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом

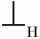
(«начало строки»), и столбца, помеченного символом c k.

10. Берем множество R t(S) для целевого символа грамматики S. Для всех терминальных символов c k, входящих в это множество, выполняем следующее: ставим знак «.>» («следует») в клетки матрицы операторного предшествования на пересечении строки, помеченной символом c k, и столбца, помеченного символом

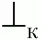
(«конец строки»). Построение матрицы закончено.

Если на всех шагах алгоритма построения матрицы операторного предшествования не возникло противоречий, когда в одну и ту же клетку матрицы надо записать два или три различных символа предшествования, то матрица построена правильно (в каждой клетке такой матрицы присутствует один из символов предшествования – «=.», «<.» или «.>» – или же клетка пуста). Если на каком-то шаге возникло противоречие, значит, исходная КС-грамматика G(VT,VN,P,S) не является грамматикой операторного предшествования. В этом случае можно попробовать преобразовать грамматику так, что она станет удовлетворять требованиям операторного предшествования (что не всегда возможно), либо необходимо использовать другой тип распознавателя.

Более подробно работа с грамматиками предшествования и другими типами распознавателей описана в [1–4, 7].

Алгоритм «сдвиг-свертка» для грамматики операторного предшествования выполняется МП-автоматом с одним состоянием. Для моделирования его работы необходима входная цепочка символов и стек символов, в котором автомат может обращаться не только к самому верхнему символу, но и к некоторой цепочке символов на вершине стека.

Этот алгоритм для заданной КС-грамматики G(VT,VN,P,S) при наличии построенной матрицы предшествования можно описать следующим образом:

1. Поместить в верхушку стека символ «начало строки», считывающую головку МП-автомата поместить в начало входной цепочки (текущим входным символом становится первый символ входной цепочки). В конец входной цепочки надо дописать символ «конец строки».

2. В стеке ищется самый верхний терминальный символ s j(если на вершине стека лежат нетерминальные символы, они игнорируются и берется первый терминальный символ, находящийся под ними), при этом сам символ s jостается в стеке. Из входной цепочки берется текущий символ a i(справа от считывающей головки МП-автомата).

3. Если символ s j– это символ начала строки, а символ a i– символ конца строки, то алгоритм завершен, входная цепочка символов разобрана.

4. В матрице предшествования ищется клетка на пересечении строки, помеченной символом s j, и столбца, помеченного символом a i(выполняется сравнение текущего входного символа и терминального символа на верхушке стека).

5. Если клетка, найденная на шаге 3, пустая, то значит, входная строка символов не принимается МП-автоматом, алгоритм прерывается и выдает сообщение об ошибке.

6. Если клетка, найденная на шаге 3, содержит символ «=.» («составляет основу») или «<.» («предшествует»), то необходимо выполнить перенос (сдвиг). При выполнении переноса текущий входной символ a iпомещается на верхушку стека, считывающая головка МП-автомата во входной цепочке символов сдвигается на одну позицию вправо (после чего текущим входным символом становится следующий символ a i +1, i:= i+ 1). После этого надо вернуться к шагу 2.

7. Если клетка, найденная на шаге 3, содержит символ «.>» («следует»), то необходимо произвести свертку. Для выполнения свертки из стека выбираются все терминальные символы, связанные отношением «=.» («составляет основу»), начиная от вершины стека, а также все нетерминальные символы, лежащие в стеке рядом с ними. Эти символы вынимаются из стека и собираются в цепочку γ (если в стеке нет символов, связанных отношением «=.», то из него вынимается один самый верхний терминальный символ и лежащие рядом с ним нетерминальные символы).