Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

Выполним необходимые дополнения и получим множества, представленные в табл. 3.3.

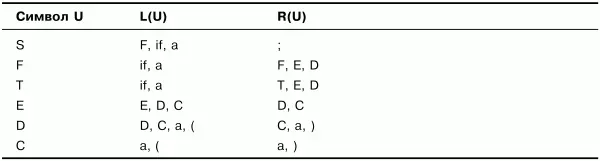
Практически все множества в табл. 3.3 изменились по сравнению с табл. 3.2 (кроме множеств для символа С), а значит, построение не закончено. Продолжим дополнять множества. Получим множества, представленные в табл. 3.4.

В табл. 3.4 по сравнению с табл. 3.3 изменились множества для символов F, Г и Е – построение не закончено. Продолжим дополнять множества. Получим множества, представленные в табл. 3.5.

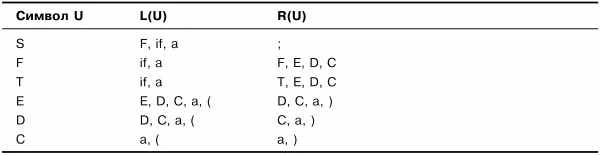
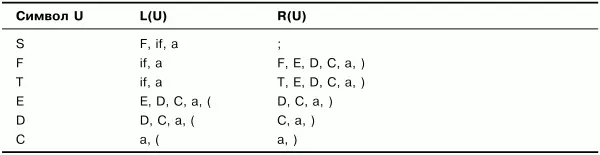
В табл. 3.5 по сравнению с табл. 3.4 изменились только множества R(U) для символов F иT– построение не закончено. Продолжим дополнять множества. Но если выполнить еще один шаг (шаг 5), то можно убедиться, что множества уже больше не изменятся (чтобы не создавать еще одну лишнюю таблицу, этот шаг здесь выполнять не будем). Таким образом, множества, представленные в табл. 3.5, являются результатом построения множеств крайних левых и крайних правых символов грамматики G.

Построение множеств крайних левых и крайних правых терминальных символов также выполним согласно описанному выше алгоритму.

На первом шаге возьмем все крайние левые и крайние правые терминальные символы из правил грамматики G. Получим множества, представленные в табл. 3.6.

Дополним множества, представленные в табл. 3.6, на основании ранее построенных множеств крайних левых и крайних правых символов, представленных в табл. 3.5. Например, L t(Е) должно быть дополнено L t(D) и L t(C), так как символы D и C входят в L(E): D, С e L(E), а R t(F) должно быть дополнено R t(E), R t(D) и R t(C), так как символы E, D и С входят в R(F): E, D, С е R(F).

Получим итоговые множества крайних левых и крайних правых терминальных символов, которые представлены в табл. 3.7.

Теперь все готово для заполнения матрицы операторного предшествования.

Для заполнения матрицы операторного предшествования необходимы множества крайних левых и крайних правых терминальных символов, представленные в табл. 3.7, и правила исходной грамматики G.

Заполнение таблицы рассмотрим на примере лексем or и (.

Символ or не стоит рядом с другими терминальными символами в правилах грамматики. Поэтому знак «=.» («составляет основу») для него не используется. Символ or стоит слева от нетерминального символа D в правиле Е → Е or D. В множество L t(D) входят символы and, а и (. Поэтому в строке матрицы, помеченной символом or, ставим знак «<.» («предшествует») в клетках на пересечении со столбцами, помеченными символами and, а и (.

Кроме того, символ or стоит справа от нетерминального символа Е в том же правиле Е → Е or D. В множество R t(E) входят символы or, xor, and, а и). Поэтому в столбце матрицы, помеченном символом or, ставим знак «.>» («следует») в клетках на пересечении со строками, помеченными символами or, xor, and, а и).

Больше ни в каких правилах символ or не встречается, поэтому заполнение матрицы для него закончено.

Символ (стоит рядом с терминальным символом) в правиле С → (Е) (между ними должно быть не более одного нетерминального символа – в данном случае один символ Е). Поэтому в строке матрицы, помеченной символом (, ставим знак «=.» («составляет основу») на пересечении со столбцом, помеченным символом).

Символ (также стоит слева от нетерминального символа Е в том же правиле С → (Е). В множество L t(E) входят символы or, xor, and, а и (. Поэтому в строке матрицы, помеченной символом (, ставим знак «<.» («предшествует») в клетках на пересечении со столбцами, помеченными символами or, xor, and, а и (.

Больше ни в каких правилах символ (не встречается, поэтому заполнение матрицы для него закончено.

Повторяя описанные выше действия по заполнению матрицы для всех терминальных символов грамматики G, получим матрицу операторного предшествования. Останется только заполнить строку, соответствующую символу «начало строки», и столбец, соответствующий символу «конец строки».

Начальным символом грамматики G является символ S, поэтому для заполнения строки, помеченной ⊥н, возьмем множество L t(S). В это множество входят символы if, а и;. Поэтому в строке матрицы, помеченной символом ⊥н, ставим знак «<.» («предшествует») в клетках на пересечении со столбцами, помеченными символами if, а и;.

Аналогично, для заполнения столбца, помеченного ⊥ к, возьмем множество R^(S). В это множество входит только один символ —;. Поэтому в столбце матрицы, помеченном символом ⊥ к, ставим знак «.>» («следует») в клетке на пересечении со строкой, помеченной символом;.

В итоге получим заполненную матрицу операторного предшествования, которая представлена в табл. 3.8.

Теперь на основе исходной грамматики G можно построить остовную грамматику G'({if,then,else,a,=,or,xor,and,(,),},{E},P',E) с правилами P':

E → E; – правило 1;

E → if E then E else E | if E then E | a:= E – правила 2, 3 и 4;

E → if E then E else E | a:= E – правила 5 и 6;

E → E or E | E xor E | E – правила 7, 8 и 9;

E → E and E | E – правила 10 и 11;

E → a | (E) – правила 12 и 13.

Жирным шрифтом в грамматике и в правилах выделены терминальные символы.

Всего имеем 13 правил грамматики. Причем правила 2 и 5, а также правила 4 и 6 в остовной грамматике неразличимы, а правила 9 и 11 не имеют смысла (как было уже сказано, цепные правила в остовных грамматиках теряют смысл). То, что две пары правил стали неразличимы, не имеет значения, так как по смыслу (семантике входного языка) эти две пары правил обозначают одно и то же (правила 2 и 5 соответствуют полному условному оператору, а правила 9 и 11 – оператору присваивания). Поэтому в дереве синтаксического разбора нет необходимости их различать. Следовательно, синтаксический распознаватель может пользоваться остовной грамматикой G'.