Миран Липовача - Изучай Haskell во имя добра!

Итак, сигнатура функции будет следующей:

quicksort :: (Ord a) => [a] –> [a]

Ничего удивительного тут нет. Базовый случай? Пустой список, как и следовало ожидать. Отсортированный пустой список – это пустой список. Затем следует основной алгоритм: отсортированный список – это список, в котором все элементы, меньшие либо равные «голове» списка, идут впереди (в отсортированном порядке), посередине следует «голова» списка, а потом – все элементы, большие «головы» списка (также отсортированные). Заметьте, в определении мы упомянули сортировку дважды, так что нам, возможно, придётся делать два рекурсивных вызова в теле функции. Также обратите внимание на то, что мы описали алгоритм, просто дав определение отсортированному списку. Мы не указывали явно: «делай это, затем делай то…» В этом красота функционального программирования! Как нам отфильтровать список, чтобы получить только те элементы, которые больше «головы» списка, и те, которые меньше? С помощью генераторов списков.

Если у нас, скажем, есть список [5,1,9,4,6,7,3]и мы хотим отсортировать его, этот алгоритм сначала возьмёт «голову», которая равна 5, и затем поместит её в середину двух списков, где хранятся элементы меньшие и большие «головы» списка. То есть в нашем примере получается следующее: [1,4,3] ++ [5] ++ [9,6,7]. Мы знаем, что когда список будет отсортирован, число 5будет находиться на четвёртой позиции, потому что есть три числа меньше и три числа больше 5. Теперь, если мы отсортируем списки [1,4,3]и [9,6,7], то получится отсортированный список! Мы сортируем эти два списка той же самой функцией. Рано или поздно мы достигнем пустого списка, который уже отсортирован – в силу своей пустоты. Проиллюстрируем (цветной вариант рисунка приведён на форзаце книги):

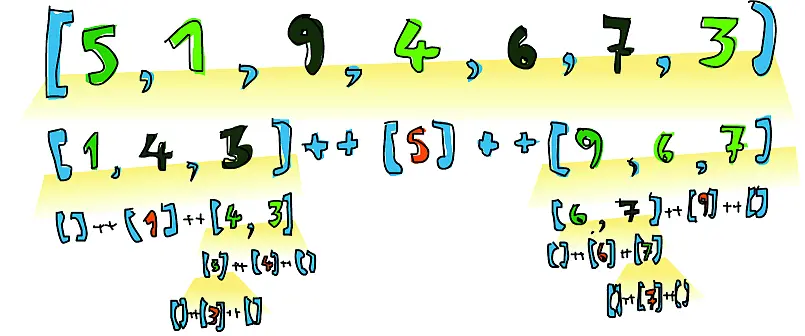
Элемент, который расположен на своём месте и больше не будет перемещаться, выделен оранжевым цветом. Если вы просмотрите элементы слева направо, то обнаружите, что они отсортированы. Хотя мы решили сравнивать все элементы с «головами», можно использовать и другие элементы для сравнения. В алгоритме быстрой сортировки элемент, с которым производится сравнение, называется опорным . На нашей картинке такие отмечены зелёным цветом. Мы выбрали головной элемент в качестве опорного, потому что его легко получить при сопоставлении с образцом. Элементы, которые меньше опорного, обозначены светло-зелёным цветом; элементы, которые больше, – темно-зелёным. Желтоватый градиент демонстрирует применение быстрой сортировки.

quicksort :: (Ord a) => [a] –> [a]

quicksort [] = []

quicksort (x:xs) =

let smallerSorted = quicksort [a | a <���– xs, a <= x]

biggerSorted = quicksort [a | a <���– xs, a > x]

in smallerSorted ++ [x] ++ biggerSorted

Давайте немного «погоняем» функцию – так сказать, испытаем её в действии:

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]

[1,2,2,3,3,4,4,5,6,7,8,9,10]

ghci> quicksort "съешь ещё этих мягких французских булок, да выпей чаю"

" ,ааабвгдеееёзииийккклмнопрсстууфхххцчшщъыьэюя"

Ура! Это именно то, чего я хотел!

Мы уже много раз использовали рекурсию, и, как вы, возможно, заметили, тут есть определённый шаблон. Обычно вы определяете базовые случаи, а затем задаёте функцию, которая что-либо делает с рядом элементов, и функцию, применяемую к оставшимся элементам. Неважно, список ли это, дерево либо другая структура данных. Сумма – это первый элемент списка плюс сумма оставшейся его части. Произведение списка – это первый его элемент, умноженный на произведение оставшейся части. Длина списка – это единица плюс длина «хвоста» списка. И так далее, и тому подобное…

Само собой разумеется, у всех упомянутых функций есть базовые случаи. Обычно они представляют собой некоторые сценарии выполнения, при которых применение рекурсивного вызова не имеет смысла. Когда имеешь дело со списками, это, как правило, пустой список. Когда имеешь дело с деревьями, это в большинстве случаев узел, не имеющий потомков.

Похожим образом обстоит дело, если вы рекурсивно обрабатываете числа. Обычно мы работаем с неким числом, и функция применяется к тому же числу, но модифицированному некоторым образом. Ранее мы написали функцию для вычисления факториала – он равен произведению числа и факториала от того же числа, уменьшенного на единицу. Такой рекурсивный вызов не имеет смысла для нуля, потому что факториал не определён для отрицательных чисел. Часто базовым значением становится нейтральный элемент. Нейтральный элемент для умножения – 1, так как, умножая нечто на 1, вы получаете это самое нечто. Таким же образом при суммировании списка мы полагаем, что сумма пустого списка равна нулю, нуль – нейтральный элемент для сложения. В быстрой сортировке базовый случай – это пустой список; он же является нейтральным элементом, поскольку если присоединить пустой список к некоторому списку, мы снова получим исходный список.

Итак, пытаясь мыслить рекурсивным образом при решении задачи, попробуйте придумать, в какой ситуации рекурсивное решение не подойдёт, и понять, можно ли использовать этот вариант как базовый случай. Подумайте, что является нейтральным элементом, как вы будете разбивать параметры функции (например, списки обычно разбивают на «голову» и «хвост» путём сопоставления с образцом) и для какой части примените рекурсивный вызов.

Функции в языке Haskell могут принимать другие функции как параметры и возвращать функции в качестве результата. Если некая функция делает что-либо из вышеперечисленного, её называют функцией высшего порядка (ФВП). ФВП – не просто одна из значительных особенностей характера программирования, присущего языку Haskell, – она по большей части и определяет этот характер. Как выясняется, ФВП незаменимы, если вы хотите программировать исходя из того, что вы хотите получить, вместо того чтобы продумывать последовательность шагов, описывающую, как это получить. Это очень мощный способ решения задач и разработки программ.

Каждая функция в языке Haskell официально может иметь только один параметр. Но мы определяли и использовали функции, которые принимали несколько параметров. Как же такое может быть? Да, это хитрый трюк! Все функции, которые принимали несколько параметров, были каррированы . Функция называется каррированной, если она всегда принимает только один параметр вместо нескольких. Если потом её вызвать, передав этот параметр, то результатом вызова будет новая функция, принимающая уже следующий параметр.