А. Григорьев - О чём не пишут в книгах по Delphi

Прежде чем искать машинное эпсилон программно, попытаемся найти его из теоретических соображений. Итак, мантисса типа Extendedсодержит 64 разряда. Чтобы закодировать единицу, старший бит мантиссы должен быть равен 1 (денормализованная запись), остальные биты — нулю. Очевидно, что при такой записи наименьшее из чисел, для которых выполняется условие x > 1, получается, когда самый младший бит мантиссы тоже будет равен единице, т.е. х = 1,00...001 (в двоичном представлении, между точкой и младшей единицей 62 нуля). Таким образом, машинное эпсилон равно х -1, т.е. 0.00...001. В более привычной десятичной форме записи это будет 2 -63, т.е. примерно 1,084·10 -19.

Листинг 3.16 показывает, как можно найти это число (пример Epsilon на компакт-диске).

procedure TForm1.Button1Click(Sender: TObject);

var

R: Extended;

I: Integer;

begin

R := 1;

while 1 + R/2 > 1 do R := R / 2;

Label1.Caption := FloatToStr(R);

end;

Запустив этот код, мы получим на экране 1.0842021724855Е-19в полном соответствии с нашими теоретическими выкладками.

В тех системах, где наблюдается описанная проблема с уменьшением точности, программа выдаст 2.22044604925031Е-16. Если вы увидели у себя это число, добавьте код, который переведет FPU в режим максимальной точности.

А теперь изменим тип переменной Rс Extendedна Double. Результат не изменится. На Single— опять не изменится. Но такое поведение лишь на первый взгляд может показаться странным. Давайте подробнее рассмотрим выражение 1 + R / 2 > 1. Итак, все вычисления (в том числе и сравнение) сопроцессор выполняет с данными типа Extended. Последовательность действий такова: число Rзагружается в регистр сопроцессора, преобразуясь при этом к типу Extended. Дальше оно делится на 2, а затем к результату прибавляется 1, и все это в Extended, никакого обратного преобразования в Single или Doubleне происходит. Затем это число сравнивается с единицей. Очевидно, что результат сравнения не должен зависеть от исходного типа R, т.к. диапазона даже типа Singleвполне хватает, чтобы разместить машинное эпсилон.

Подведем итоги сказанному. Значения, которые мы получаем, могут отличаться от ожидаемых, даже если речь идет о простом присваивании. Во многих случаях (например, в научных расчетах) это несущественно, т.к. сам метод расчета дает еще большую погрешность. Проблемы начинаются там, где мы хотим вывести число на экран или сравнить его с другим. Универсальных рецептов на все случаи жизни не существует, но во многих ситуациях помогают следующие советы:

□ Если ваша задача — просто получить "красивое" представление числа на экране, то функцию FloatToStrзаменяйте на ее более мощный аналог FloatToStrFили на функцию Format— они позволяют указать желаемое количество символов после точки.

□ Сравнение вещественных чисел следует выполнять с учетом погрешности, т.е. вместо if а = b… писать if Abs(а - b) < Ерs…, где Eps— некоторая величина, задающая допустимую погрешность (в модуле Math, начиная с Delphi 6, существует функция SameValue, с помощью которой это же условие можно записать как if SameValue(a, b, Eps)…).

□ Для денежных расчетов следует выбирать тип Currency, реализующий число с фиксированной, а не плавающей, десятичной точкой. Отметим также, что не следует пытаться решить проблему неточного представления числа (0,100000001490116 вместо 0,1) с помощью функции RoundTo, поскольку эта функция не может обеспечить точность бо́льшую, чем точность аппаратного представления вещественных чисел.

В этом разделе мы рассмотрим некоторые тонкости работы со строками, которые позволяют лучше понять, какой код генерирует компилятор при некоторых, казалось бы, элементарных действиях. Не все приведенные здесь примеры работают не так, как можно было бы ожидать, так что этот материал немного выходит за рамки главы. Но "подводные камни" здесь мы тоже встретим.

Для работы с кодировкой ANSI в Delphi существует три вида строк: AnsiString, ShortStringи PChar. Различие между ними заключается в способе хранения строки, а также выделения и освобождения памяти для нее. Зарезервированное слово stringпо умолчанию означает тип AnsiString, но если после нее следует число в квадратных скобках, то это означает тип ShortString, а число — ограничение по длине. Кроме того, существует опция компилятора Huge strings(управляется также директивами компилятора {$H+/-}и {$LONGSTRINGS ON/OFF}, которая по умолчанию включена, но если ее выключить, то слово stringстанет эквивалентно ShortString; или, что то же самое, string[255]. Эта опция введена для обратной совместимости с Turbo Pascal, в новых программах отключать ее нет нужды. Внутреннее устройство этих типов данных иллюстрирует рис. 3.2.

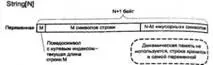
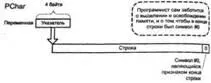
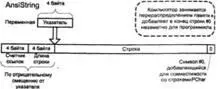
Рис. 3.2. Устройство различных строковых типов Delphi

Наиболее просто устроен тип ShortString. Это массив символов с индексами от 0 до N , где N — число символов, указанное при объявлении переменной (в случае использования идентификатора ShortString N явно не указывается и равно 255). Нулевой элемент массива хранит текущую длину строки, которая может быть меньше или равна объявленной (эту длину мы будем далее обозначать M ), элементы с индексами от 1 до M — это символы, составляющие строку. Значения элементов с индексами M +1.. N не определены. Все стандартные функции для работы со строками игнорируют эти символы. В памяти такая переменная всегда занимает N +1 байтов.

Ограничения типа ShortStringочевидны: на хранение длины отводится только один байт, поэтому такая строка не может содержать больше 255 символов. Кроме того, такой способ записи длины не совпадает с принятым в Windows, поэтому ShortStringнесовместим с системными строками.

В системе приняты так называемые нуль-терминированные строки: строка передается указателем на ее первый символ, длина строки отдельно нигде не хранится, признаком конца строки считается встретившийся в цепочке символов #0. Длина таких строк ограничена только доступной памятью и способом адресации (т.е. в Windows теоретически это 4 294 967 295 символов). Для работы с такими строками предусмотрен тип PChar. Переменная такого типа является указателем на начало строки. В литературе нередко можно встретить утверждение, что PChar = ^Сhar, однако это неверно: тип PCharвстроен в компилятор и не выводится из других типов. Это позволяет выполнять с ним операции, недопустимые для других указателей. Во-первых, если P — переменная типа PChar, то допустимо обращение к отдельным символам строки с помощью конструкции P[N], где N— целочисленное выражение, определяющее номер символа (в отличие от типа ShortString, здесь символы нумеруются с 0, а не с 1). Во-вторых, к указателям типа PCharразрешено добавлять и вычитать целые числа, смещая указатель на соответствующее число байтов вверх или вниз (здесь речь идет только об операторах "+" и "-"; адресная арифметика с помощью процедур Inc иDec доступна для любых типизированных указателей, а не только для PChar).