А. Григорьев - О чём не пишут в книгах по Delphi

Теперь переведем эти правила на язык БНФ (листинг 4.1).

::= [] {}

[ {}]

[ [] {}]

::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

::= '+' | '-'

::= '.'

::= 'E' | 'e'

На основе этих правил можно написать функцию IsNumber, которая в качестве параметра принимает строку и возвращает True, если эта строка удовлетворяет правилам записи числа, и False, если не удовлетворяет (листинг 4.2).

// Проверка символа на соответствие

function IsDigit(Ch: Char): Boolean;

begin

Result := Ch in ['0'..'9'];

end;

// Проверка символа на соответствие

function IsSign(Ch: Char): Boolean;

begin

Result := (Ch = '+') or (Ch = '-');

end;

// Проверка символа на соответствие

function IsSeparator(Ch: Char): Boolean;

begin

Result := Ch='.';

end;

// Проверка символа на соответствие

function IsExponent(Ch: Char): Boolean;

begin

Result := (Ch = 'E') or (Ch = 'e');

end;

function IsNumber(const S: string): Boolean;

var

P: Integer; // Номер символа выражения, который сейчас проверяется

begin

Result := False;

// Проверка, что выражение содержит хотя бы один символ — пустая строка

// не является числом

if Length(S) = 0 then Exit;

// Начинаем проверку с первого символа

Р := 1;

// Если первый символ — , переходим к следующему

if IsSign(S[Р]) then Inc(Р);

// Проверяем, что в данной позиции стоит хотя бы одна цифра

if (Р > Length(S)) or not IsDigit(S[Р]) then Exit;

// Переходим к следующей позиции, пока не достигнем конца строки

// или не встретим не цифру

repeat

Inc(Р);

until (Р > Length(S)) or not IsDigit(S[Р]);

// Если достигли конца строки, выражение корректно — число.

// не имеющее дробной части и экспоненты

if Р > Length(S) then

begin

Result := True;

Exit;

end;

// Если следующей символ — , проверяем, что после него

// стоит хотя бы одна цифра

if IsSeparator(S[P]) then

begin

Inc(P);

if (P > Length(S)) or not IsDigit(S[P]) then Exit;

repeat

Inc(P);

until (P > Length(S)) or not IsDigit(S[P]);

// Если достигли конца строки, выражение корректно — число

// без экспоненты

if Р > Length(S) then

begin

Result := True;

Exit;

end;

end;

// Если следующий символ — , проверяем, что после него

// стоит все то, что требуется правилами

if IsExponent(S[Р]) then

begin

Inc(P);

if P > Length(S) then Exit;

if IsSign(S[P]) then Inc(P);

if (P > Length(S)) or not IsDigit(S[P]) then Exit;

repeat

Inc(P);

until (P > Length(S)) or not IsDigit(S[P]);

if P > Length(S) then

begin

Result := True;

Exit;

end;

end;

// Если выполнение дошло до этого места, значит, в выражении остались

// еще какие-то символы. Так как никакие дополнительные символы

// синтаксисом не предусмотрены, такое выражение не считается

// корректным числом.

end;

Для каждого нетерминального символа мы ввели отдельную функцию, разбор начинается с символа самого верхнего уровня — — и следует правилам, записанным для этого символа. Такой способ синтаксического анализа называется левосторонним рекурсивным нисходящим анализом . Левосторонним потому, что символы в выражении перебираются слева направо, нисходящим — потому, что сначала анализируются символы верхнего уровня, а потом — символы нижнего. Рекурсивность метода на данном примере не видна, т. к. наша грамматика не содержит рекурсивных определений, но мы с этим столкнемся в последующих примерах.

Пример использования функции IsNumberсодержится на компакт-диске и называется IsNumberSample.

В заключение рассмотрим альтернативный способ записи грамматики вещественного числа — графический (такой способ называется синтаксическим графом, или рельсовой диаграммой). Это направленный граф, узлами которого являются терминальные (круги) и нетерминальные (прямоугольники) символы. Двигаться от одного узла к другому можно только по линиям в направлениях, указанных стрелками. В таком графе достаточно легко разобраться, а по возможностям описания синтаксиса он эквивалентен БНФ. На рис. 4.1 показана запись синтаксиса вещественного числа с помощью рельсовой диаграммы.

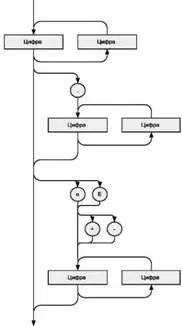
Рис. 4.1.Диаграмма синтаксиса вещественного числа

В качестве самостоятельного упражнения рекомендуем нарисовать с помощью рельсовой диаграммы грамматику символа "Цифра", используемого на рис. 4.1.

Теперь у нас уже достаточно знаний, чтобы создать простейший калькулятор, т. е. функцию, которая будет на входе принимать выражение, а на выходе, если это выражение корректно, возвращать результат его вычисления. Для начала ограничимся простым калькулятором, который умеет работать только с числовыми константами и знает только четыре действия арифметики. Изменение порядка вычисления операторов с помощью скобок также оставим на потом.

Таким образом, наш калькулятор будет распознавать и вычислять цепочки чисел, между которыми стоят знаки операции, которые над этими числами выполняются. В вырожденном случае выражение может состоять из одного числа и, соответственно, не содержать ни одного знака операции. Опишем эти правила с помощью БНФ и ранее определенного символа .

::= { }

::= '+' | '-' | '*' | '/'

В нашей грамматике не предусмотрено, что между оператором и его операндами может находиться пробел, т.е. выражение "2 + 2", в отличие от "2+2", не удовлетворяет данной грамматике. В отсутствие лексического анализатора игнорирование пробелов и прочих разделителей (переводов строки, комментариев) является трудоемкой рутинной операцией, поэтому во всех примерах без лексического анализатора мы будем требовать, чтобы выражения не содержали пробелов.

Для написания калькулятора нам понадобятся две новых функции — IsOperator, которая проверяет, является ли следующий символ оператором, и Expr, которая получает на входе строку, анализирует ее в соответствии с указанными правилами и вычисляет результат. Кроме того, функция IsNumberсама по себе нам тоже больше не нужна — мы создадим на ее основе функцию Number, которая получает на входе строку и номер позиции, начиная с которой в этой строке должно быть расположено число, проверяет, так ли это, и возвращает это число. Кроме того, функция Numberдолжна перемещать указатель на следующий после числа символ строки, чтобы функция Expr, вызвавшая Number, могла узнать, с какого символа продолжать анализ. Если последовательность символов не является корректным числом, функция Numberвозбуждает исключение ESyntaxError, определенное специально для указания на ошибку в записи выражения.