Иван Братко - Программирование на языке Пролог для искусственного интеллекта

• если X < M1, то поиск продолжается в левом поддереве, иначе

• если X < M2, то поиск продолжается в среднем поддереве, иначе —

• в правом поддереве.

Если в корне находится только одна метка М, то переходим к левому поддереву при X < M и к правому поддереву — в противоположном случае. Продолжаем применять сформулированные выше правила, пока не окажемся на самом нижнем уровне дерева, где и выяснится, найден ли элемент X, или же поиск потерпел неудачу.

Так как все листья 2-3 дерева находятся на одном и том же уровне, 2-3 дерево идеально сбалансировано с точки зрения глубины составляющих его поддеревьев. Все пути от корня до листа, которые мы проходим при поиске, имеют одну и ту же длину порядка log n , где n — число элементов, хранящихся в дереве.

При добавлении нового элемента данных 2-3 дерево может расти не только в глубину, но и в ширину. Каждая внутренняя вершина, имеющая два поддерева, может приобрести новое поддерево, что приводит к росту вширь. Если же, с другой стороны, у вершины уже есть три поддерева, и она должна принять еще одно, то она расщепляется на две вершины, каждая из которых берет на себя по два из имеющихся четырех поддеревьев. Образовавшаяся при этом новая вершина передается вверх по дереву для присоединения к одной из выше расположенных вершин. Если же эта ситуация возникает на самом высоком уровне, то дерево вынуждено "вырасти" на один уровень вверх. Рис. 10.3 иллюстрирует описанный принцип.

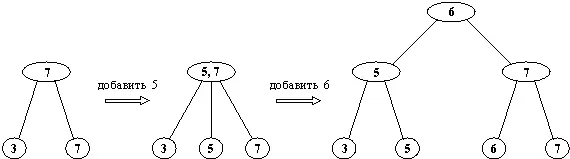
Рис. 10.3. Вставление нового элемента в 2-3 справочник. Дерево растет сначала вширь, а затем уже вглубь.

Включение нового элемента в 2-3 справочник мы запрограммируем как отношение

доб23( Дер, X, НовДер)

где дерево НовДерполучено введением элемента Xв дерево Дер. Основную работу мы поручим двум дополнительным отношениям, которые мы назовем встав. Первое из них имеет три аргумента:

встав( Дер, X, НовДер).

Здесь НовДер — результат вставления элемента Xв Дер. Деревья Дери НовДеримеют одну и ту же глубину . Разумеется, не всегда возможно сохранить ту же глубину дерева. Поэтому существует еще одно отношение с пятью аргументами специально для этого случая:

встав( Дер, X, НДа, Mб, НДб).

Имеется в виду, что при вставления Xв Дердерево Дерразбивается на два дерева НДаи НДб, имеющих ту же глубину, что и Дер. Мб — это минимальный элемент из НДб. Пример показан на рис. 10.4.

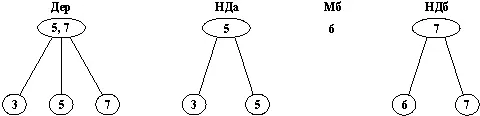
Рис. 10.4. Объекты, показанные на рисунке, удовлетворяют отношению встав( Дер, 6, НДа, Мб, НДб).

2-3 деревья мы будем представлять в программе следующим образом:

• nilпредставляет пустое дерево;

• л( X)представляет дерево, состоящее из одной вершины — листа с элементом X;

• в2( Д1, М, Д2)представляет дерево с двумя поддеревьями Д1 и Д2; M — минимальный элемент из Д2;

• в3( Д1, M2, Д2, М3, Д3)представляет дерево с тремя поддеревьями Д1, Д2 и Д3; M2 — минимальный элемент из Д2; М3 — минимальный элемент из Д3; Д1, Д2 и Д3 — 2-3 деревья.

Между доб23и вставсуществует следующая связь: если после вставления нового элемента дерево не "вырастает", то

доб23( Дер, X, НовДер) :-

встав( Дер, X, НовДер).

Однако если после вставления элемента глубина дерева увеличивается, то вставпорождает два поддерева Д1 и Д2, а затем составляет из них дерево большей глубины:

доб23( Дер, X, в2( Д1, М, Д2) ) :-

встав( Дер, X, Д1, М, Д2).

Отношение вставустроено более сложным образом, поскольку ему приходится иметь дело со многими случаями, а именно вставление в пустое дерево, в дерево, состоящее из одного листа, и в деревья типов в2 и в3. Возникают также дополнительные подслучаи, так как новый элемент можно вставить в первое, либо во второе, либо в третье поддерево. В связи с этим мы определим вставкак набор правил таким образом, чтобы каждое предложение процедуры вставимело дело с одним из этих случаев. На рис. 10.5 показаны некоторые из возможных случаев. На Пролог они транслируются следующим образом:

Случай а

встав( в2( Д1, M, Д2), X, в2( НД1, M, Д2) ) :-

больше( M, X), % M больше, чем X

встав( Д1, X, НД1).

Случай b

встав( в2( Д1, M, Д2), X, в3( НД1а, Мб, НД1б, M, Д2) ) :-

больше( M, X),

встав( Д1, X, НД1а, Мб, НД1б).

Случай с

встав( в3( Д1, M2, Д2, М3, Д3), X,

в2( НД1а, Мб, НД1б), M2, в2(Д2, М3, Д3) ) :-

больше( M2, X),

встав( Д1, X, НД1а, Мб, НД1б).

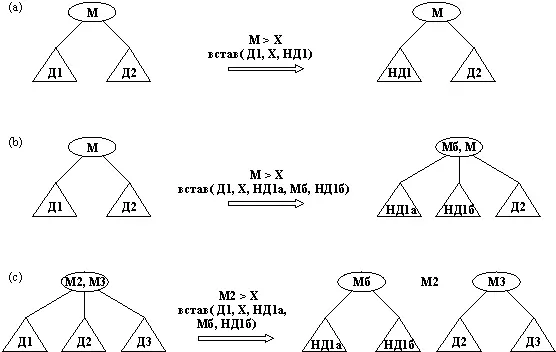
Рис. 10.5.Некоторые из случаев работы отношения встав . (a) встав( в2( Д1, М, Д2), X, в2( НД1, М, Д2) ); (b) встав( в2( Д1, М, Д2), X, в3( НД1а, Мб, НД1б, М, Д2) ); (c) встав( в3( Д1, M2, Д2, М3, Д3), X, в2( НД1а, Мб, НД1б), M2, в2( Д2, М3, Д3) ).

% Вставление элемента в 2-3 справочник

доб23( Дер, X, Дер1) :- % Вставить X в Дер, получить Дер1

встав( Дер, X, Дер1). % Дерево растет вширь

доб23( Дер, X, в2( Д1, M2, Д2) ) :-

встав( Дер, X, Д1, M2, Д2). % Дерево растет вглубь

доб23( nil, X, л( X) ).

встав( л( А), X, л( А), X, л( X) ) :-

больше( X, А).

встав( л( А), X, л( X), А, л( А) ) :-

больше( А, X).

встав( в2( Д1, М, Д2), X, в2( НД1, М, Д2) ) :-

больше( М, X),

встав( Д1, X, НД1).

встав( в2( Д1, М, Д2), X, в3( НД1а, Мб, НД1б, М, Д2) ) :-

больше( М, X),

встав( Д1, X, НД1а, Мб, НД1б).

встав( в2( Д1, М, Д2), X, в2( Д1, М, НД2) ) :-

больше( X, М),

встав( Д2, X, НД2).

встав( в2( Д1, М, Д2), X, в3( Д1, М, НД2а, Мб, НД2б) ) :-

больше( X, М),

встав( Д2, X, НД2а, Мб, НД2б).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в3( НД1, M2, Д2, М3, Д3) :-

больше( M2, X),

встав( Д1, X, НД1).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в2( НД1а, Мб, НД1б), M2, в2( Д2, М3, Д3) ) :-

больше( M2, X),

встав( Д1, X, НД1а, Мб, НД1б).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в3( Д1, M2, НД2, М3, Д3) ) :-

больше( X, M2), больше( М3, X),

встав( Д2, X, НД2).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в2( Д1, M2, НД2а), Мб, в2( НД2б, М3, Д3) ) :-

больше( X, M2), больше( М3, X),

встав( Д2, X, НД2а, Мб, НД2б).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в3( Д1, M2, Д2, М3, НД3) ) :-

больше( X, М3),

встав( Д3, X, НД3).

встав( в3( Д1, M2, Д2, М3, Д3), X,

в2( Д1, M2, Д2), М3, в2( НД3а, Мб, НД3б) ) :-

больше( X, М3),