Иван Братко - Программирование на языке Пролог для искусственного интеллекта

10.3. Определите отношение

avl( Дер)

для проверки того, является ли ДерAVL-деревом, т.е. верно ли, что любые два его поддерева, подсоединенные к одной и той же вершине, отличаются по глубине не более чем на 1. Двоичные деревья представляйте в виде термов д( Лев, Кор, Прав)или nil .

% Вставление элемента в AVL-справочник

доб_аvl( nil/0, X, д( nil/0, X, nil/0)/1).

% Добавить X к пустому дереву

доб_аvl( д( L, Y, R)/Ну, X, НовДер) :-

% Добавить X к непустому дереву

больше( Y, X),

доб_аvl( L, X, д( L1, Z, L2)/ _ ),

% Добавить к левому поддереву

соединить( L1, Z, L2, Y, R, НовДер).

% Сформировать новое дерево

доб_avl( д( L, Y, R)/Ну, X, НовДер) :-

больше( X, Y),

доб_avl( R, X, д( R1, Z, R2)/ _ ),

% Добавить к правому поддереву

соединить( L1, Y, Rl, Z, R2, НовДер).

соединить( Д1/Н1, А, д( Д21, В, Д22)/Н2, С, Д3/Н3,

д( д( Д1/Н1, А, Д21)/На, В, д( Д22, С, L3/Н3)/Нс)/Нb) :-

Н2 > H1, H2 > Н3, % Среднее дерево глубже остальных

На is H1 + 1,

Hс is Н3 + 1,

Нb is На + 1.

соединить( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3,

д( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3)/Нс)/На) :-

H1 >= H2, H1 >= Н3, % "Глубокое" левое дерево

max1( H2, Н3, Нс),

max1( H1, Нс, На).

соединить( Д1/Н1, А, Д2/Н2, С, Д3/Н3,

д( д( Д1/Н1, А, Д2/Н2)/На, С, Д3/Н3)/Нс) :-

Н3 >= H2, Н3 >= H1, % "Глубокое" правое дерево

max1( H1, H2, На),

max1( На, Н3, Нс).

max1( U, V, М) :-

U > V, !, М is U + 1; % М равно 1 плюс max( U, V)

М is V + 1.

Рис. 10.10. Вставление элемента в AVL-справочник. В этой программе предусмотрено, что попытка повторного вставления элемента терпит неудачу. По поводу процедуры соединитьсм. рис. 10.9.

• 2-3 деревья и AVL-деревья, представленные в настоящей главе, — это примеры сбалансированных деревьев.

• Сбалансированные или приближенно сбалансированные деревья гарантируют эффективное выполнение трех основных операций над деревьями: поиск, добавление и удаление элемента. Время выполнения этих операций пропорционально log n , где n — число вершин дерева.

2-3 деревья детально описаны, например, в Aho, Hopcroft and Ullman (1974, 1983). В книге этих авторов, вышедшей в 1983 г., дается также реализация соответствующих алгоритмов на языке Паскаль. H.Вирт (см. Wirth (1976)) приводит программу на Паскале для работы с AVL-деревьями. 2-3 деревья являются частным случаем более общего понятия В-деревьев. В-деревья, а также несколько других вариантов структур данных, имеющих отношение к 2-3 деревьям в AVL-деревьям, рассматриваются в книге Gonnet (1984). В этой книге, кроме того, даны результаты анализа поведения этих структур.

Программа вставления элемента в AVL-дерево, использующая только величину "перекоса" дерева (т.е. значение разности глубин поддеревьев, равной -1, 0 или 1, вместо самой глубины) опубликована ван Эмденом (1981).

Aho А. V., Hopcroft J. E. and Ullman J. D. (1974). The Design and Analysis of Computer Algorithms. Addison-Wesley. [Имеется перевод: Ахо А., Хопкрофт Дж. Построение и анализ вычислительных алгоритмов. Пер. с англ. — М.: Мир, 1979.]

Aho А. V., Hopcroft J. E. and Ullman J. D. (1983). Data Structures and Algorithms. Addison-Wesley.

Gonnet G. H. (1984). Handbook of Algorithms + Data Structures. Addison-Wesley.

van Emden M. (1981). Logic Programming Newsletter 2.

Wirth N. (1976). Algorithms + Data Structures = Programs. Prentice-Hall. [Имеется перевод: Вирт H. Алгоритмы + структуры данных = программы. — M.: Мир, 1985.]

В данной главе мы сосредоточим свое внимание на одной общей схеме для представления задач, называемой пространством состояний . Пространство состояний — это граф, вершины которого соответствуют ситуациям, встречающимся в задаче ("проблемные ситуации"), а решение задачи сводится к поиску пути в этом графе. Мы изучим на примерах, как формулируются задачи в терминах пространства состояний, а также обсудим общие методы решения задач, представленных в рамках этого формализма. Процесс решения задачи включает в себя поиск в графе, при этом, как правило, возникает проблема, как обрабатывать альтернативные пути поиска. В этой главе будут представлены две основные стратегии перебора альтернатив, а именно поиск в глубину и поиск в ширину.

Рассмотрим пример, представленный на рис. 11.1. Задача состоит в выработке плана переупорядочивания кубиков, поставленных друг на друга, как показано на рисунке. На каждом шагу разрешается переставлять только один кубик. Кубик можно взять только тогда, когда его верхняя поверхность свободна. Кубик можно поставить либо на стол, либо на другой кубик. Для того, чтобы построить требуемый план, мы должны отыскать последовательность ходов, реализующую заданную трансформацию.

Эту задачу можно представлять себе как задачу выбора среди множества возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить кубик С на стол. После того как кубик С поставлен на стол, мы имеем три альтернативы:

• поставить А на стол или

• поставить А на С, или

• поставить С на А.

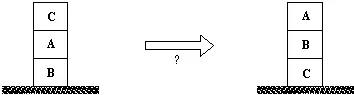
Рис. 11.1. Задача перестановки кубиков.

Ясно, что альтернативу "поставить С на стол" не имело смысла рассматривать всерьез, так как этот ход никак не влияет на ситуацию.

Как показывает рассмотренный пример, с задачами такого рода связано два типа понятий:

(1) Проблемные ситуации.

(2) Разрешенные ходы или действия, преобразующие одни проблемные ситуации в другие.

Проблемные ситуации вместе с возможными ходами образуют направленный граф, называемый пространством состояний . Пространство состояний для только что рассмотренного примера дано на рис. 11.2. Вершины графа соответствуют проблемным ситуациям, дуги — разрешенным переходам из одних состояний в другие. Задача отыскания плана решения задачи эквивалентна задаче построения пути между заданной начальной ситуацией ("стартовой" вершиной) и некоторой указанной заранее конечной ситуацией, называемой также целевой вершиной .

На рис. 11.3 показан еще один пример задачи: головоломка "игра в восемь" в ее представление в виде задачи поиска пути. В головоломке используется восемь перемещаемых фишек, пронумерованных цифрами от 1 до 8. Фишки располагаются в девяти ячейках, образующих матрицу 3 на 3. Одна из ячеек всегда пуста, и любая смежная с ней фишка может быть передвинута в эту пустую ячейку. Можно сказать и по-другому, что пустой ячейке разрешается перемещаться, меняясь местами с любой из смежных с ней фишек. Конечная ситуация — это некоторая заранее заданная конфигурация фишек, как показано на рис. 11.3.