Иван Братко - Программирование на языке Пролог для искусственного интеллекта

• Теорема о допустимости помогает установить, всегда ли А*-алгоритм, использующий некоторую конкретную эвристическую функцию, находит оптимальное решение.

Программа поиска с предпочтением, представленная в настоящей главе, — это один из многих вариантов похожих друг на друга программ, из которых А*-алгоритм наиболее популярен. Общее описание А*-алгоритма можно найти в книгах Nillson (1971, 1980) или Winston (1984). Теорема о допустимости впервые доказана авторами статьи Hart, Nilsson, and Raphael (1968). Превосходное и строгое изложение многих разновидностей алгоритмов поиска с предпочтением и связанных с ними математических результатов дано в книге Pearl (1984). В статье Doran and Michie (1966) впервые изложен поиск с предпочтением, управляемый оценкой расстояния до цели.

Головоломка "игра в восемь" использовалась многими исследователями в области искусственного интеллекта в качестве тестовой задачи при изучении эвристических принципов (см., например, Doran and Michie (1966), Michie and Ross (1970) и Gaschnig (1979)).

Задача планирования, рассмотренная в настоящей главе, также как и многие ее разновидности, возникает во многих прикладных областях в ситуации, когда необходимо спланировать обслуживание запросов на ресурсы. Один из примеров — операционные системы вычислительных машин. Задача планирования со ссылкой на это конкретное приложение изложена в книге Coffman and Denning (1973).

Найти хорошую эвристику — дело важное и трудное, поэтому изучение эвристик — одна из центральных тем в искусственном интеллекте. Существуют, однако, некоторые границы, за которые невозможно выйти, двигаясь в направлении улучшения качества эвристик. Казалось бы, все, что необходимо для эффективного решения комбинаторной задачи — это найти мощную эвристику. Однако есть задачи (в том числе многие задачи планирования), для которых не существует универсальной эвристики, обеспечивающей во всех случаях как эффективность, так и допустимость. Многие теоретические результаты, имеющие отношение к этому ограничению, собраны в работе Garey and Johnson (1979).

Coffman E.G. and Denning P.J. (1973). Operating Systems Theory. Prentice-Hall.

Doran J. and Michie D. (1966). Experiments with the graph traverser program. Proc. Royal Socieiy of London 294(A): 235-259.

Garey M. R. and Johnson D. S. (1979). Computers and Intractability . W. H. Freeman. [Имеется перевод: Гэри M., Джонсон Д. С- Вычислительные машины и труднорешаемые задачи. — M.: Мир, 1982.]

Gaschnig J. (1979). Performance measurement and analysis of certain search algorithms. Carnegie-Mellon University: Computer Science Department-Technical Report CMU-CS-79-124 (Ph. D. Thesis).

Hart P.E., Nilsson N.J. and Raphael B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Sciences and Cybernetics SSC-4(2):100-107

Michie D. and Ross R. (1970). Experiments with the adaptive graph traverser. Machine Intelligence 5: 301–308.

Nilsson N.J. (1971). Problem — Solving Methods in Artificial Intelligence . McGraw-Hill. [Имеется перевод: Нильсон H. Искусственный интеллект. Методы поиска решений. — M: Мир, 1973.]

Nilsson N. J. (1980). Principles of Artificial Intelligence . Tioga; also Springer-Verlag.

Pearl J. (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving . Addison-Wesley.

Winston P. H. (1984). Artificial Intelligence (second edition). Addison-Wesley. [Имеется перевод первого издания: Уинстон П. Искусственный интеллект. — M.: Мир, 1980.]

Представление в виде И/ИЛИ-графов наиболее хорошо приспособлено для задач, которые естественным образом разбиваются на взаимно независимые подзадачи. Примерами таких задач могут служить поиск маршрута, символическое интегрирование, а также игровые задачи, доказательство теорем и т.п. В этой главе мы разработаем программы для поиска в И/ИЛИ-графах, в том числе программу поиска с предпочтением, управляемого эвристиками.

В главах 11 и 12, говоря о решении задач, мы сконцентрировали свое внимание на пространстве состояний как средстве представления этих задач. В соответствии с таким подходом решение задач сводилось к поиску пути в графе пространства состояний. Однако для некоторых категорий задач представление в форме И/ИЛИ-графа является более естественным. Такое представление основано на разбиении задач на подзадачи. Разбиение на подзадачи дает преимущества в том случае, когда подзадачи взаимно независимы, а, следовательно, и решать их можно независимо друг от друга.

Проиллюстрируем это на примере. Рассмотрим задачу отыскания на карте дорог маршрута между двумя заданными городами, как показано на рис. 13.1. Не будем пока учитывать длину путей. Разумеется, эту задачу можно сформулировать как поиск пути в пространстве состояний. Соответствующее пространство состояний выглядело бы в точности, как карта рис. 13.1: вершины соответствуют городам, дуги — непосредственным связям между городами. Тем не менее давайте построим другое представление, основанное на естественном разбиении этой задачи на подзадачи.

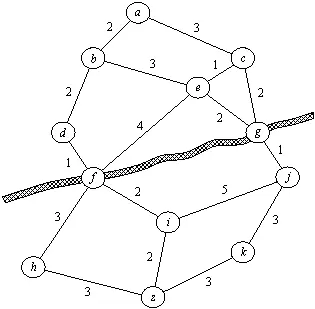
Рис. 13.1. Поиск маршрута из а в z на карте дорог. Через реку можно переправиться в городах f и g . И/ИЛИ-представление этой задачи показано на рис. 13.2.

На карте рис. 13.1 мы видим также реку. Допустим, что переправиться через нее можно только по двум мостам: один расположен в городе f , другой — в городе g . Очевидно, что искомый маршрут обязательно должен проходить через один из мостов, а значит, он должен пройти либо через f , либо через g . Таким образом, мы имеем две главных альтернативы:

Для того, чтобы найти путь из а в z , необходимо найти одно из двух :

(1) путь из а в z , проходящий через f , или

(2) путь из а в z , проходящий через g .

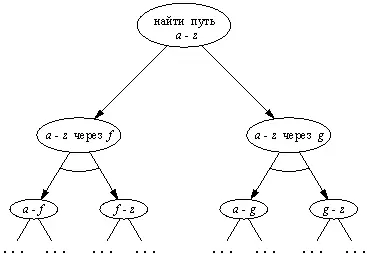
Рис. 13.2. И/ИЛИ-представление задачи поиска маршрута рис. 13.1. Вершины соответствуют задачам или подзадачам, полукруглые дуги означают, что все (точнее, обе) подзадачи должны быть решены.

Теперь каждую из этих двух альтернативных задач можно, в свою очередь, разбить следующим образом:

(1) Для того, чтобы найти путь из a в z через f , необходимо:

1.1 найти путь из а и f и

1.2 найти путь из f в z .

(2) Для того, чтобы найти путь из a в z через g , необходимо:

2.1 найти путь из а в g и

2.2 найти путь из g в z .

Рис. 13.3. (а) Решить P — это значит решить P 1 или Р 2 или … (б) Решить Q — это значит решить все: Q 1 и Q 2 и ….

Итак, мы имеем две главных альтернативы для решения исходной задачи: (1) путь через f или (2) путь через g . Далее, каждую из этих альтернатив можно разбить на подзадачи (1.1 и 1.2 или 2.1 и 2.2 соответственно). Здесь важно то обстоятельство, что каждую из подзадач в обоих альтернативах можно решать независимо от другой. Полученное разбиение исходной задачи можно изобразить в форме И/ИЛИ-графа (рис. 13.2). Обратите внимание на полукруглые дуги, которые указывают на отношение И между соответствующими подзадачами. Граф, показанный на рис. 13.2 — это всего лишь верхняя часть всего И/ИЛИ-дерева. Дальнейшее разбиение подзадач можно было бы строить на основе введения дополнительных промежуточных городов.