Иван Братко - Программирование на языке Пролог для искусственного интеллекта

После распространения поиска из первоначального дерева (снимок А) получается дерево В. Вершина а — это ИЛИ-вершина, поэтому мы имеем два решающих дерева-кандидата: b и с . Поскольку F( b) = 1 < 3 = F( c) , для продолжения поиска выбирается альтернатива b . Насколько далеко может зайти процесс роста поддерева b ? Этот процесс может продолжаться до тех пор, пока не произойдет одно из двух событий:

(1) F -оценка вершины b станет больше, чем F -оценка ее конкурента с , или

(2) обнаружится, что найдено решающее дерево.

В связи с этим, начиная просмотр поддерева-кандидата b , мы устанавливаем верхнюю границу для F( b) : F( b) ≤ 3 = F( c) . Сначала порождаются преемники d и e вершины b (снимок С),после чего F -оценка b возрастает до 3. Так как это значение не превосходит верхнюю границу, рост дерева-кандидата с корнем в b продолжается. Вершина d оказывается целевой вершиной, а после распространения поиска из вершины e на один шаг получаем дерево, показанное на снимке D. В этот момент выясняется, что F( b) = 9 > 3 , и рост дерева b прекращается. В результате процесс поиска не успевает "осознать", что h — это тоже целевая вершина и что порождено решающее дерево. Вместо этого происходит переключение активности на конкурирующую альтернативу с . Поскольку в этот момент F( b) = 9, устанавливается верхняя граница для F( c) , равная 9. Дерево-кандидат с корнем с наращивается (с учетом установленного ограничения) до тех пор, пока не возникает ситуация, показанная на снимке E. Теперь процесс поиска обнаруживает, что найдено решающее дерево (включающее в себя целевые вершины h и g ), на чем поиск заканчивается. Заметьте, что в качестве результата процесс поиска выдает наиболее дешевое из двух возможных решающих деревьев, а именно решающее дерево рис. 13.4(с).

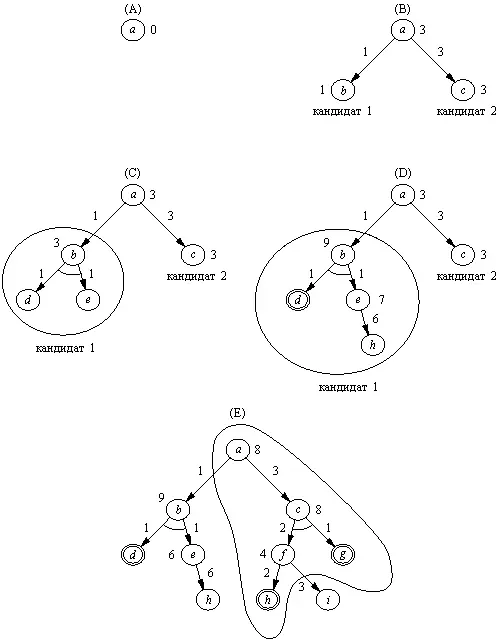
Рис. 13.10. Трассировка процесса поиска с предпочтением в И/ИЛИ-графе ( h = 0) при решении задачи рис. 13.4.

Программа, в которой реализованы идеи предыдущего раздела, показана на рис. 13.12. Прежде, чем мы перейдем к объяснению отдельных деталей этой программы, давайте рассмотрим тот способ представления дерева поиска, который в ней используется.

Существует несколько случаев, как показано на рис. 13.11. Различные формы представления поискового дерева возникают как комбинации следующих возможных вариантов, относящихся к размеру дерева и к его "решающему статусу".

• Размер:

(1) дерево состоит из одной вершины (листа) или

(2) оно имеет корень и (непустые) поддеревья.

• Решающий статус:

(1) обнаружено, что дерево соответствует решению задачи (т.е. является решающим деревом) или

(2) оно все еще решающее дерево- кандидат .

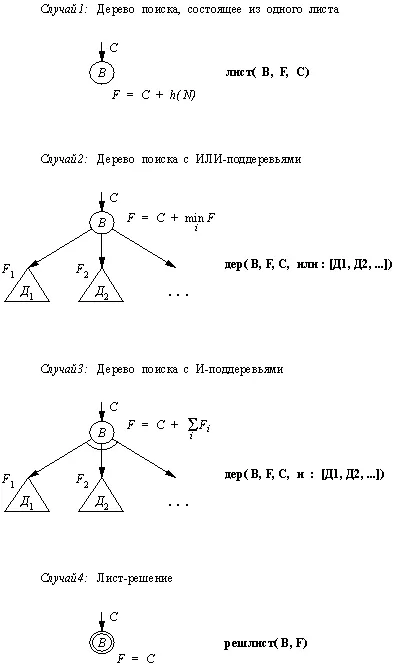
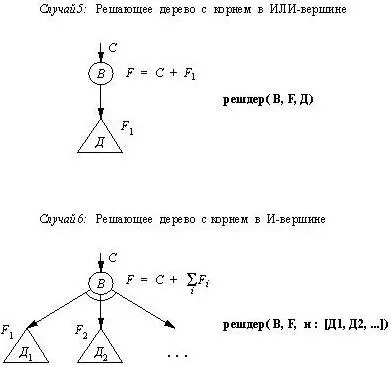
Рис. 13.11. Представление дерева поиска.

Основной функтор, используемый для представления дерева, указывает, какая из комбинаций этих воз-можностей имеется в виду. Это может быть одна из следующих комбинаций:

лист решлист дер решдер

Далее, в представление дерева входят все или некоторые из следующих объектов:

• корневая вершина дерева,

• F -оценка дерева,

• стоимость С дуги И/ИЛИ-графа, ведущей в корень дерева,

• список поддеревьев,

• отношение (И или ИЛИ) между поддеревьями.

Список поддеревьев всегда упорядочен по возрастанию F -оценок. Поддеревья, являющиеся решающими деревьями, помещаются в конец списка.

Обратимся теперь к программе рис. 13.12. Отношение самого высокого уровня — это

и_или( Верш, РешДер)

где Верш — стартовая вершина. Программа строит решающее дерево (если таковое существует), рассчитывая на то, что оно окажется оптимальным решением. Будет ли это решение в действительности самым дешевым, зависит от той функции h , которую использует алгоритм. Существует теорема, в которой говорится о том, как оптимальность решения зависит от h . Эта теорема аналогична теореме о допустимости алгоритма поиска с предпочтением в пространстве состояний (гл. 12). Обозначим через С( В) стоимость оптимального решающего дерева для вершины В . Если для каждой вершины В И/ИЛИ-графа эвристическая оценка h(B) ≤ C(B) , то гарантируется, что процедура и_или найдет оптимальное решение. Если же h не удовлетворяет этому условию, то найденное решение может оказаться субоптимальным. Существует тривиальная эвристическая функция, удовлетворяющая условию оптимальности, а именно h = 0 для всех вершин. Ее недостатком является отсутствие эвристической силы.

Основную роль в программе рис. 13.12 играет отношение

расширить( Дер, Предел, Дер1, ЕстьРеш)

Дери Предел — его "входные" аргументы, а Дер1и ЕстьРеш — "выходные". Аргументы имеют следующий смысл:

Дер — дерево поиска, подлежащее расширению.

Предел — предельное значение F -оценки, при котором еще разрешено наращивать дерево Дер.

ЕстьРеш — индикатор, значения которого указывают на то, какой из следующих трех случаев имеет место:

(1) ЕстьРеш = да: Дерможно "нарастить" (с учетом ограничения Предел) таким образом, чтобы образовалось решающее дерево Дер1.

(2) ЕстьРеш = нет: дерево Дерможно расширить до состояния Дер1, для которого F -оценка превосходит Предел, но прежде чем F -оценка превзошла Предел, решающее дерево не было обнаружено.

(3) ЕстьРеш = никогда: Дерне содержит решения.

В зависимости от случая Дер1 — это либо решающее дерево, либо Дер, расширенное до момента перехода через Предел; если ЕстьРеш = никогда, то переменная Дер1неинициализирована.

Процедура

расширспис( Деревья, Предел, Деревья1, ЕстьРеш)

аналогична процедуре расширить. Так же, как и в процедуре расширить, Пределзадает ограничение на рост дерева, а ЕстьРеш — это индикатор, указывающий, каков результат расширения ("да", "нет" или "никогда"). Первый аргумент — это, на этот раз, список деревьев (И-список или ИЛИ-список):

Деревья = или:[Д1, Д2, ...]или

Деревья = и : [Д1, Д2, ...]

Процедура расширсписвыбирает из списка Деревьянаиболее перспективное дерево (исходя из F -оценок). Так как деревья в списке упорядочены, таким деревом является первый элемент списка. Наиболее перспективное дерево подвергается расширению с новым ограничением Предел1. Значение Предел1зависит от Предел, а также от других деревьев списка. Если Деревья — это ИЛИ-список, то Предел1устанавливается как наименьшая из двух величин: Предели F -оценка следующего по "качеству" дерева из списка Деревья. Если Деревья — это И-дерево, то Предел1устанавливается равным Пределминус сумма F -оценок всех остальных деревьев из списка. Значение переменной Деревья1зависит от случая, задаваемого индикатором ЕстьРеш. Если ЕстьРеш = нет, то Деревья1 — это то же самое, что и список Деревья, причем наиболее перспективное дерево расширено с учетом ограничения Предел1. Если ЕстьРеш = да, то Деревья1 — это решение для всего списка Деревья(найденное без выхода за границы значения Предел). Если ЕстьРеш = никогда, то переменная Деревья1неинициализирована.