Иван Братко - Программирование на языке Пролог для искусственного интеллекта

имитация_в_ширину( Верш, РешДер) :-

проба_в_глубину( Верш, РешДер, 0).

% Проба поиска с возрастающим ограничением, начиная с 0

проба_в_глубину( Верш, РешДер, Глуб) :-

решить( Верш, РешДер, Глуб);

Глуб1 is Глуб + 1, % Новый предел по глубине

проба_в_глубину( Верш, РешДер, Глуб1).

% Попытка с новым ограничением

Недостатком имитации поиска в ширину является то, что при каждом увеличении предела по глубине программа повторно просматривает верхнюю область пространства поиска.

13.1. Закончите составление программы поиска в глубину (с ограничением) для И/ИЛИ-графов, намеченную в настоящем разделе.

13.2. Определите на Прологе И/ИЛИ-пространство для задачи "ханойская башня" и примените к нему процедуры поиска настоящего раздела.

13.3. Рассмотрите какую-нибудь простую детерминированную игру двух лиц с полной информацией и дайте определение ее И/ИЛИ-представления. Используйте программу поиска в И/ИЛИ-графах для построения выигрывающих стратегий в форме И/ИЛИ-деревьев.

Базовые процедуры поиска предыдущего раздела производят систематический и полный просмотр И/ИЛИ-дерева, не руководствуясь при этом какими-либо эвристиками. Для сложных задач подобные процедуры весьма не эффективны из-за большой комбинаторной сложности пространства поиска. В связи с этим возникает необходимость в эвристическом управлении поиском, направленном на уменьшение комбинаторной сложности за счет исключения бесполезных альтернатив. Управление эвристиками, излагаемое в настоящем разделе, будет основано на численных эвристических оценках "трудности" задач, входящих в состав И/ИЛИ-графа. Программу, которую мы составим, можно рассматривать как обобщение программы поиска с предпочтением в пространстве состояний гл. 12.

Начнем с того, что сформулируем критерий оптимальности, основанный на стоимостях дуг И/ИЛИ-графа. Во-первых, мы расширим наше представление И/ИЛИ-графов, дополнив его стоимостями дуг. Например, И/ИЛИ-граф рис. 13.4 можно представить следующими предложениями:

а ---> или : [b/1, с/3].

b ---> и : [d/1, e/1].

с ---> и : [f/2, g/1].

e ---> или : [h/6].

f ---> или : [h/2, i/3].

цель( d). цель( g). цель( h).

Стоимость решающего дерева мы определим как сумму стоимостей его дуг. Цель оптимизации - найти решающее дерево минимальной стоимости. Как и раньше, иллюстрацией служит рис. 13.4.

Будет полезным определить стоимость вершины И/ИЛИ-графа как стоимость оптимального решающего дерева для этой вершины. Стоимость вершины, определенная таким образом, соответствует "трудности" соответствующей задачи.

Мы будем предполагать, что стоимости вершин И/ИЛИ-графа можно оценить (не зная соответствующих решающих деревьев) при помощи эвристической функции h . Эти оценки будут использоваться для управления поиском. Наша программа поиска начнет свою работу со стартовой вершины и, распространяя поиск из уже просмотренных вершин на их преемников, будет постепенно наращивать дерево поиска. Этот процесс будет строить дерево даже в том случае, когда сам И/ИЛИ-граф не является деревом; при этом граф будет разворачиваться в дерево за счет дублирования своих отдельных частей.

Для продолжения поиска будет всегда выбираться "наиболее перспективное" решающее дерево-кандидат. Каким же образом используется функция h для оценки степени перспективности решающего дерева-кандидата или, точнее, вершины-кандидата — корня этого дерева?

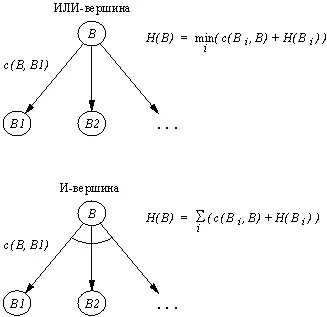
Рис. 13.9. Получение оценки H трудности задач И/ИЛИ-графа.

Обозначим через H(В) оценку трудности вершины В . Для самой верхней вершины текущего дерева поиска H(В) просто совпадает с h(В) . С другой стороны, для оценки внутренней вершины дерева поиска нам не обязательно использовать непосредственно значение h , поскольку у нас есть некоторая дополнительная информация об этой вершине: мы знаем ее преемников. Следовательно, как показано на рис. 13.9, мы можем приближенно оценить трудность внутренней ИЛИ-вершины как

где с(В, В i) — стоимость дуги, ведущей из В в В i . Взятие минимума в этой формуле оправдано тем обстоятельством, что для того, чтобы решить задачу В , нам нужно решить только одну из ее задач-преемников. Трудность И-вершины В можно приближенно оценить так:

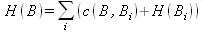
Будем называть H -оценку внутренней вершины "возвращенной" (backed-up) оценкой.

Более практичной с точки зрения использования в нашей программе поиска является другая величина F , которую можно определить в терминах H следующим образом. Пусть В1 — вершина-предшественник вершины В в дереве поиска, причем стоимость дуги, ведущей из В1 в В , равна с(В1, В) , тогда положим

F( B) = с( В1, В) + H( В)

Пусть В1 — родительская вершина вершины В , а В 1, В 2, … — ее дочерние вершины, тогда, в соответствии с определениями F и H , имеем

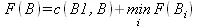, если В — ИЛИ-вершина

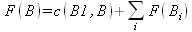, если В — И-вершина

Хотя стартовая вершина А и не имеет предшественника, будем считать, что стоимость ведущей в нее (виртуальной) дуги равна 0. Если положить h равным 0 для всех вершин И/ИЛИ-дерева, то для любого найденного оптимального решающего дерева окажется, что его стоимость, т.е. сумма стоимостей его дуг, в точности равна F(A) .

На любой стадии поиска каждый преемник ИЛИ-вершины соответствует некоторому альтернативному решающему дереву-кандидату. Процесс поиска всегда принимает решение продолжать просмотр того дерева-кандидата, для которого F -оценка минимальна. Вернемся еще раз к рис. 13.4 и посмотрим, как будет вести себя процесс, поиска на примере И/ИЛИ-графа, изображенного на этом рисунке. В начале дерево поиска состоит всего из одной вершины — стартовой вершины а , далее дерево постепенно "растет" до тех пор, пока не будет найдено решающее дерево. На рис. 13.10, показан ряд "мгновенных снимков", сделанных в процессе роста дерева поиска. Для простоты мы предположим, что h = 0 для всех вершин. Числа, приписанные вершинам на рис. 13.10 — это их F -оценки (разумеется, по мере накопления информации в процессе поиска они изменяются). Ниже даются некоторые пояснительные замечания к рис. 13.10.