Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Одна большая проблема, связанная с пузырьковой сортировкой, да и честно говоря, со многими другими алгоритмами, состоит в том, что переставляются только соседние элементы. Если элемент с наименьшим значением оказывается в самом конце списка, он будет меняться местами с соседними элементами до тех пор, пока он не достигнет первой позиции.

Пузырьковая сортировка относится к нестабильным алгоритмам, поскольку из двух элементов с равными значениями первым в отсортированном списке будет тот, который находился в исходном списке дальше от начала. Если изменить тип сравнения на "меньше чем" или "равен", а не просто "меньше", тогда пузырьковая сортировка станет устойчивой, но количество перестановок увеличится, и введенная нами оптимизация не даст запланированного выигрыша в скорости.

Пузырьковая сортировка имеет одну малоизвестную вариацию, которая на практике дает незначительное увеличение скорости, - это так называемая шейкер-сортировка (shaker sort).

Рисунок 5.2. Два прохода с помощью шейкер-сортировки

Вернемся к картам. Выполните первый проход согласно алгоритму сортировки. Туз попадет на первую позицию. Теперь, вместо прохода колоды карт справа налево, пройдите слева направо: сравните вторую и третью карты и старшую карту поместите на третью позицию. Сравните третью и четвертую карты, и при необходимости поменяйте их местами. Продолжайте сравнения вплоть до достижения пары (12, 13). По пути к правому краю колоды вы "захватили" короля и переместили его на последнюю позицию.

А теперь снова пройдите колоду справа налево до второй карты. Во вторую позицию попадет двойка. Продолжайте чередовать направления проходов до тех пор, пока не будет отсортирована вся колода.

Листинг 5.5. Шейкер-сортировка

procedure TDShakerSort(aList :TList;

aFirst : integer; aLast : integer;

aCompare : TtdCompareFunc);

var

i : integer;

Temp : pointer;

begin

TDValidateListRange(aList, aFirst, aLast, 'TDShakerSort');

while (aFirst < aLast) do

begin

for i := aLast downto succ(aFirst) do

if (aCompare(aList.List^[i], aList.List^[i-1]) < 0) then begin

Temp := aList.List^[i];

aList.List^[i] := aList.List^[i-1];

aList.List^[i-1] := Temp;

end;

inc(aFirst);

for i := succ(aFirst) to aLast do

if (aCompare(aList.List^[i], aList.List^[i-1]) < 0) then begin

Temp := aList.List^[i];

aList.List^[i] := aList.List^[i-1];

aList.List^[i-1] := Teilend;

dec(aLast);

end;

end;

Несмотря на то что шейкер-сортировка принадлежит к алгоритмам класса O(n(^2^)), время ее выполнения немного меньше, чем для пузырьковой сортировки. Причина, по которой алгоритм назван именно шейкер-сортировкой, состоит в том, что элементы в списке колеблются относительно своих позиций до тех пор, пока список не будет отсортирован.

Как и пузырьковая сортировка, шейкер-сортировка относится к неустойчивым алгоритмам.

Следующим алгоритмом, который мы рассмотрим, будет сортировка методом выбора (selection sort). Это пока что первый метод, который действительно можно использовать в повседневной практике (о пузырьковой сортировке и шейкер-сортировке можно уже забыть).

Начиная с правого края колоды, просмотрите все карты и найдите самую младшую (конечно, это будет туз). Поменяйте местами туз с первой картой. Теперь, игнорируя первую карту, снова просмотрите всю колоду справа налево в поисках самой младшей карты. Поменяйте местами младшую карту со второй картой. Далее, игнорируя первые две карты, просмотрите всю колоду справа налево в поисках самой младшей карты и поменяйте найденную карту с третьей картой. Продолжайте процесс до тех пор, пока вся колода не будет отсортирована. Очевидно, что тринадцатый цикл не понадобится, поскольку он будет манипулировать только с одной картой, которая к тому времени уже будет находиться в требуемой позиции.

Листинг 5.6. Сортировка методом выбора

procedure TDSelectionSort(aList : TList;

aFirst : integer; aLast : integer;

aCompare : TtdCompareFunc);

var

i, j : integer;

IndexOfMin : integer;

Temp : pointer;

begin

TDValidateListRange(aList, aFirst, aLast, 'TDSelectionSort');

for i := aFirst to pred(aLast) do

begin

IndexOfMin := i;

for j := succ(i) to aLast do

if (aCompare(aList.List^[j], aList.List^[IndexOfMin]) < 0) then

IndexOfMin := j;

if (aIndexOfMin <> i) then begin

Temp := aList.List^[i];

aList.List^[i] := aList.List^[IndexOfMin];

aList.List^[IndexOfMin] := Teilend;

end;

end;

Рисунок 5.3 Сортировка методом выбора

Как видите, в приведенном коде снова присутствуют два вложенных цикла, следовательно, сортировка методом выбора относится к алгоритмам класса O(n(^2^)). В первом цикле индекс проходит значения от aFast до aLast-1 и при каждом его выполнении во внутреннем цикле определяется элемент с минимальным значением в оставшейся части списка. В отличие от нашего примера с картами, внутренний цикл заранее не знает, каковым будет минимальный элемент в списке, поэтому ему нужно просмотреть все элементы. После обнаружения минимального элемента он переставляется в требуемую позицию.

Сортировка методом выбора интересна одной своей особенностью. Количество выполняемых сравнений для первого прохода равно n, для второго - n-1 и т.д. Общее количество сравнений будет равно n (n + 1)/2 = 1, т.е. сортировка принадлежит к классу алгоритмов O(n(^2^)). Тем не менее, количество перестановок намного меньше: при каждом выполнении внешнего цикла производится всего одна перестановка. Таким образом, общее количество перестановок (n - 1), т.е. O(n). Что это означает на практике? Если стоимость перестановки элементов намного больше, чем время сравнения (под стоимостью в данном случае понимается время или требуемые ресурсы), сортировка методом выбора оказывается достаточно эффективной.

Сортировка методом выбора относится к группе устойчивых алгоритмов. Поиск наименьшего значения будет возвращать первое в списке наименьшее значение из нескольких имеющихся. Таким образом, равные значения будут находиться в отсортированном списке в том же порядке, в котором они были в исходном списке.

И последний алгоритм из первого рассматриваемого нами набора - сортировка методом вставок, или сортировка простыми вставками (Insertion sort). Этот алгоритм покажется знакомым всем, кто играет в такие карточные игры, как вист или бридж, поскольку большинство игроков сортирует свои карты именно так.

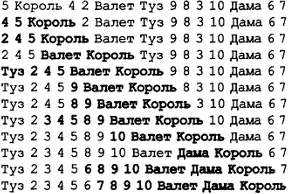
Рисунок 5.4. Стандартная сортировка методом вставок

Начинаем с левого края колоды. Сравниваем две первые карты и располагаем их в правильном порядке. Смотрим на третью карту. Вставляем ее в требуемое место по отношению к первым двум картам. Смотрим на четвертую карту и вставляем ее в требуемое место по отношению к первым трем картам. Те же операции выполняем с пятой, шестой, седьмой и всеми последующими картами. При перемещении слева направо левая часть колоды будет отсортированной.