Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Выполнение сортировки методом Шелла на примере карточной колоды требует немало усилий, но не будем терять времени. Разложите колоду в длинную линию. Извлеките из колоды первую и каждую четвертую карту после первой (т.е., пятую, девятую и тринадцатую). Выполните сортировку выбранных карт с помощью метода вставок и снова поместите все карты в колоду. Извлеките из колоды вторую и каждую четвертую карту после второй (т.е., шестую и десятую). Выполните сортировку выбранных карт с помощью метода вставок и снова поместите все карты в колоду. Выполните те же операции над третьей и каждой четвертой картой после третьей, а затем над четвертой и каждой четвертой картой после четвертой.

После первого прохода карты будут находиться в отсортированном порядке по 4. Какую бы карту вы не выбрали, карты, которые находятся на количество позиций, кратном 4 вперед и назад, будут отсортированы в требуемом порядке. Обратите внимание, что карты в целом не отсортированы, но, тем не менее, независимо от исходного положения карт, после первого прохода они будут находиться недалеко от своих мест в отсортированной последовательности.

Теперь выполним стандартную сортировку методом вставок, в результате чего получим отсортированную колоду карт. Как уже говорилось, при небольших расстояниях между элементами в исходном списке и их позициями в отсортированном списке (что мы и получили после первого прохода) быстродействие сортировки методом вставок линейно зависит от числа элементов.

Говоря более строгим языком, сортировка методом Шелла работает путем вставки отсортированных подмножеств основного списка. Каждое подмножество формируется за счет выборки каждого h-ого элемента, начиная с любой позиции в списке. В результате будет получено h подмножеств, которые отсортированы методом вставок. Полученная последовательность элементов в списке называется отсортированной по h. Затем значение к уменьшается и снова выполняется сортировка. Уменьшение значение к происходит до тех пор, пока к не будет равно 1, после чего последний проход будет представлять собой стандартную сортировку методом вставок (которая, если быть точным, представляет собой сортировку по 1).

Суть сортировки методом Шелла заключается в том, что сортировка по h быстро переносит элементы в область, где они должны находиться в отсортированном списке, а уменьшение значения к позволяет постепенно уменьшать размер "прыжков" и, в конце концов, поместить элемент в требуемую позицию. Медленному перемещению элементов предшествуют большие "скачки", сводящиеся к простой сортировке методом вставок, которая практически не передвигает элементы.

Какие значения к лучше всего использовать? Шелл в своей первой статье на эту тему предложил значения 1, 2, 4, 8, 16, 32 и т.д. (естественно, в обратном порядке), но с этими значениями связана одна проблема: до последнего прохода элементы с четными индексами никогда не сравниваются с элементами с нечетными индексами. И, следовательно, при выполнении последнего прохода все еще возможны перемещения элементов на большие расстояния (представьте себе, например, искусственный случай, когда элементы с меньшими значениями находятся в позициях с четными индексами, а элементы с большими значениями - в позициях с нечетными индексами).

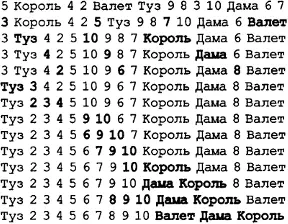
Рисунок 5.6. Сортировка методом Шелла

В 1969 году Дональд Кнут (Donald Knuth) предложил последовательность 1, 4, 13, 40, 121 и т.д. (каждое последующее значение на единицу больше, чем утроенное предыдущее значение). Для списков средних размеров эта последовательность позволяет получить достаточно высокие характеристики быстродействия (на основе эмпирических исследований Кнут оценил быстродействие для среднего случая как O(n(^5/4^)), а для худшего случая было доказано, что скорость работы равна O(n(^3/2^))) при несложном методе вычисления значений самой последовательности. Ряд других последовательностей позволяют получить более высокие значения скорости работы (хотя и не намного), но требуют предварительного вычисления значений последовательности, поскольку используемые формулы достаточно сложны. В качестве примера можно привести самую быструю известную на сегодняшний день последовательность, разработанную Робертом Седжвиком (Robert Sedgewick): 1, 5, 19, 41, 109 и т.д. (формируется путем слияния двух последовательностей — 9 * 4i - 9 * 2i + 1 для i > 0 и 4i - 3 * 2i + 1 для i > 1). Известно, что для этой последовательности время работы в худшем случае определяется как O(n(^4/3^)) при O(n(^7/6^)) для среднего случая. В этой книге мы не будем приводить математические выкладки для определения приведенных зависимостей. Пока не известно, существуют ли еще более быстрые последовательности. (подробнейшие выкладки и анализ всех фундаментальных алгоритмов, в числе которых и алгоритмы, рассмотренные в данной книге, а также эффективная их реализация на языках С, С++ и Java, можно найти в многотомниках Роберта Седжвика "Фундаментальные алгоритмы на С++", "Фундаментальные алгоритмы на С" и "Фундаментальные алгоритмы на Java", которые выпущены издательством "Диасофт".)

Листинг 5.9. Сортировка методом Шелла при использовании последовательности Кнута

procedure TDShellSort(aList : TList;

aFirst : integer;

aLast : integer;

aCompare : TtdCompareFunc);

var

i, j : integer;

h : integer;

Temp : pointer;

Ninth : integer;

begin

TDValidateListRange(aList, aFirst, aLast, 'TDShellSort');

{прежде всего вычисляем начальное значение h; оно должно быть близко к одной девятой количества элементов в списке}

h := 1;

Ninth := (aLast - aFirst) div 9;

while (h<= Ninth) do h := (h * 3) + 1;

{начать выполнение цикла, который при каждом проходе уменьшает значение h на треть}

while (h > 0) do

begin

{выполнить сортировку методом вставки для каждого подмножества}

for i := (aFirst + h) to aLast do

begin

Temp := aList.List^[i];

j := i;

while (j >= (aFirst+h)) and

(aCompare(Temp, aList.List^[j-h]) < 0) do

begin

aList.List^[j] := aList.List^[j-h];

dec(j, h);

end;

aList.List^[j ] := Teilend;

{уменьшить значение h на треть}

h := h div 3;

end;

end;

Математические зависимости для анализа быстродействия сортировки методом Шелла достаточно сложны. В общем случае для оценки времени выполнения сортировки при различных значениях h приходится ограничиваться статистическими данными. Тем не менее, анализ быстродействия алгоритма Шелла практически не имеет смысла, поскольку существуют более быстрые алгоритмы.

Что касается устойчивости, то при перестановке элементов, далеко отстоящих друг от друга, возможно нарушение порядка следования элементов с равными значениями. Следовательно, сортировка методом Шелла относится к группе неустойчивых алгоритмов.