Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Result := Node;

end;

procedure TtdBinarySearchTree.Delete(aItem : pointer);

begin

FBinTree.Delete(bstFindNodeToDelete(aItem));

dec(FCount);

end;

Большая часть работы выполняется методом bstFindNodeToDelete. Он вызывает метод bstFindItem, чтобы найти элемент, который требуется удалить (естественно, если он не найден, генерируется ошибка), а затем проверяет, имеет ли найденный узел два дочерних узла. Если имеет, мы ищем узел с наибольшим элементом, который меньше удаляемого элемента. Мы меняем местами элементы в узлах и возвращаем второй элемент.

Как обычно, дерево бинарного поиска будет реализовано в виде класса, хотя хотелось бы еще раз предупредить, что его следует использовать только в том случае, если есть уверенность, что вставляемые элементы являются в достаточной степени случайными или их количество достаточно мало, чтобы дерево не выродилось в длинную вытянутую структуру. Основное назначение класса дерева бинарного поиска - попытка сокрытия от пользователя внутренней структуры дерева. Это означает, что пользователь должен иметь возможность использовать класс для поддержания набора элементов в отсортированном порядке и выполнения их обхода без необходимости знания структуры внутренних узлов.

При реализации дерева бинарного поиска мы не будем использовать наследование от класса бинарного поиска, описанного в первой части этой главы. В основном, это обусловлено тем, что класс бинарного дерева открывает пользователю слишком много подробностей внутренней структуры узлов. Вместо этого мы делегируем функции вставки, удаления и обхода внутреннему объекту бинарного дерева. Просто на тот случай, если пользователю потребуется знание внутреннего объекта дерева, мы откроем его через соответствующее свойство.

Листинг 8.16. Интерфейс дерева бинарного поиска

type

TtdBinarySearchTree = class {класс дерева бинарного поиска}

private

FBinTree : TtdBinaryTree;

FCompare : TtdCompareFunc;

FCount : integer;

FName : TtdNameString;

protected

procedure bstError(aErrorCode : integer;

const aMethodName : TtdNameString);

function bstFindItem(aItem : pointer; var aNode : PtdBinTreeNode;

var aChild : TtdChildType): boolean;

function bstFindNodeToDelete(aItem : pointer): PtdBinTreeNode;

function bstInsertPrim(aItem : pointer; var aChildType : TtdChildType): PtdBinTreeNode;

public

constructor Create( aCompare : TtdCompareFunc;

aDispose : TtdDisposeProc);

destructor Destroy; override;

procedure Clear;

procedure Delete(aItem : pointer); virtual;

function Find(aKeyItem : pointer): pointer; virtual;

procedure Insert(aItem : pointer); virtual;

function Traverse( aMode : TtdTraversalMode;

aAction : TtdVisitProc; aExtraData : pointer;

aUseRecursion : boolean): pointer;

property BinaryTree : TtdBinaryTree read FBinTree;

property Count : integer read FCount;

property Name : TtdNameString read FName write FName;

end;

Глядя на определение этого класса, легко убедиться, что мы уже встречались с большинством методов.

Исходный код класса TtdBinarySearchTree можно найти на Web-сайте издательства, в разделе материалов. После выгрузки материалов отыщите среди них файл TDBinTre.pas.

В ходе рассмотрения дерева бинарного поиска неоднократно упоминалось, что добавление элементов в дерево бинарного поиска может сделать его крайне несбалансированным, а иногда даже привести к его вырождению в длинное вытянутое дерево, подобное связному списку.

Проблема этого вырождения заключается не в том, что дерево перестает корректно функционировать (элементы продолжают храниться в отсортированном порядке), а в том, что в данном случае эффективности древовидной структуры наносится, по сути, смертельный удар. Для идеально сбалансированного дерева (в котором все родительские узлы имеют по два дочерних узла, а все листья размещаются на одном уровне, плюс-минус один) время поиска, время вставки и время удаления соответствуют O(log(n)). Иначе говоря, если для выполнения основной операции в дереве с 1000 узлов требуется время, равное t, для ее выполнения в дереве с 1000000 узлов потребуется время равное всего лишь 2t. С другой стороны время выполнения базовых операций в вырожденном дереве пропорционально O(n), и, следовательно, для выполнения этой же операции в дереве с 1 000 000 узлов потребовалось бы время, равное 1000t.

Так каким же образом избежать этого вырождения деревьев? Ответ заключается в создании алгоритма, который осуществляет балансировку дерева бинарного поиска во время вставки и удаления элементов. Прежде чем действительно приступить к рассмотрению алгоритмов балансировки, давайте исследуем различные методы перекомпоновки деревьев бинарного поиска, а затем ими можно будет воспользоваться для балансировки деревьев.

Вспомните, что в дереве бинарного поиска все узлы в левом дочернем дереве данного узла меньше, а узлы в правом дочернем дереве больше его. (Естественно, под тем, что один узел меньше другого, подразумевается, что ключ элемента в одном узле меньше ключа элемента в другом узле. Просто проще написать, что "один узел меньше другого", нежели постоянно ссылаться на ключи узлов.) Немного проанализируем эту аксиому.

Взгляните на левый дочерний узел в дереве бинарного поиска. Что мы знаем о нем? Что ж, естественно, он имеет собственные левое и правое дочерние деревья. Он больше всех узлов в его левом дочернем дереве и меньше всех узлов в правом дочернем дереве. Более того, поскольку он является левым дочерним узлом, его родительский узел больше всех узлов в его правом дочернем дереве. Следовательно, если повернуть левый дочерний узел в позицию его родительского узла, чтобы его правое дочернее дерево стало новым левым дочерним деревом родительского узла, результирующее бинарное дерево останется допустимым. Этот поворот показан на рис. 8.3. На этом рисунке треугольники представляют дочерние деревья, которые содержат ноль или больше узлов - для алгоритма поворота точное их количество роли не играет.

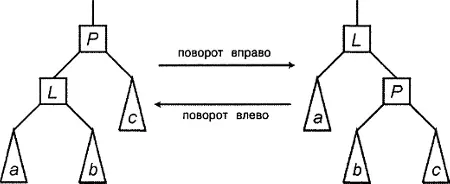
Рисунок 8.3. Повышение ранга левого дочернего узла (и наоборот)

Для исходного дерева можно было бы записать следующее неравенство: (а < L < b) < P < с. Для нового дерева имеем: a< L< (b< P< c), что, конечно же, остается справедливым и при удалении круглых скобок, поскольку операция < подчиняется коммуникативному закону. (первое неравенство читается следующим образом: все узлы в дереве а меньше узла L, который меньше всех узлов в дереве b, а все это дерево в целом меньше узла P, который, в свою очередь, меньше всех узлов в дереве с. Подобным же образом можно интерпретировать и второе неравенство.)

Только что рассмотренную операцию называют поворотом вправо (right rotation). При этом говорят, что ранг левого дочернего узла L повышается, а ранг родительского узла P понижается. Иначе говоря, узел L перемещается на один уровень вверх, а узел P - на один уровень вниз. Такой поворот называется поворотом вокруг узла P.