Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Естественно, рассмотрев поворот вправо, легко предположить, как выполняется другой поворот, поворот влево (left rotation), который создал бы первое дерево из второго. Поворот влево повышает ранг правого дочернего узла P и понижает ранг родительского узла L. Код выполнения обеих видов поворота приведен в листинге 8.17, при этом кодирование выполняется с точки зрения того узла, ранг которого повышается.

Листинг 8.17. Повышение ранга узла

function TtdSplayTree.stPromote(aNode : PtdBinTreeNode): PtdBinTreeNode;

var

Parent : PtdBinTreeNode;

begin

{пометить родительский узел того узла, ранг которого повышается}

Parent := aNode^.btParent;

{в обеих случаях необходимо разорвать и перестроить шесть связей: связь узла с его дочерним узлом и противоположную связь, связь узла с его родительским узлом и противоположную связь и связь родительского узла с его родительским узлом и противоположную связь; обратите внимание, что дочерний узел данного узла может быть пустым}

{повысить ранг левого дочернего узла, т.е. выполнить поворот родительского узла вправо}

if (Parent^.btChild[ctLeft] = aNode) then begin

Parent^.btChild[ctLeft] := aNode^.btChild[ctRight];

if (Parent^.btChild[ctLeft] <> nil) then

Parent^.btChild[ctLeft]^.btParent := Parent;

aNode^.btParent := Parent^.btParent;

if (aNode^.btParent^.btChild[ctLeft] = Parent) then

aNode^.btParent^.btChild[ctLeft] := anode else

aNode^.btParent^.btChild[ctRight] := aNode;

aNode^.btChild[ctRight] := Parent;

Parent^.btParent := aNode;

end

{повысить ранг правого дочернего узла, т.е. выполнить поворот родительского узла влево}

else begin

Parent^.btChild[ctRight] := aNode^.btChild[ctLeft];

if (Parent^.btChild[ ctRight ] <> nil) then

Parent^.btChild[ctRight]^.btParent := Parent;

aNode^.btParent := Parent^.btParent;

if (aNode^.btParent^.btChild[ctLeft] = Parent) then

aNode^.btParent^.btChild[ctLeft] := anode else

aNode^.btParent^.btChild[ctRight] := aNode/ aNode^.btChild[ctLeft] := Parent;

Parent^.btParent := aNode;

end;

{вернуть узел, ранг которого был повышен}

Result := aNode;

end;

Этот метод заимствован из класса скошенного дерева, который будет рассматриваться несколько позже. А пока важно отметить способ разрыва и преобразования связей, используемый для выполнения обоих типов повышения ранга. Поскольку переданный методу узел может быть левым или правым дочерним узлом, имеющим различные связи, которые необходимо разорвать и перестроить, по существу, этот метод представляет собой оператор If, учитывающий две возможности.

Два рассмотренных вида поворота реорганизуют дерево на локальном уровне, но основное свойство упорядоченности узлов дерева бинарного поиска остается неизменным. В случае выполнения поворота вправо все узлы дерева а перемещаются на один уровень ближе к корневому узлу, те, которые расположены в дереве b, остаются на том же уровне, а расположенные в дереве с, перемещаются на один уровень вниз. При выполнении поворота влево все узлы дерева а перемещаются на один уровень дальше от корневого узла, узлы дерева b остаются на том же уровне, а узлы дерева с перемещаются на один уровень вверх. Несложно догадаться, что, управляя некоторым общим алгоритмом балансировки, с помощью последовательности этих двух поворотов можно было бы восстановить баланс в дереве бинарного поиска.

Часто эти два вида поворота объединяются попарно и используются в формах так называемых спаренных двухсторонних поворотов (zig-zag) и спаренных односторонних поворотов (zig-zig). Существуют две операции спаренного двустороннего поворота и две операции спаренного одностороннего поворота. Операция спаренного двустороннего поворота состоит либо из поворота вправо, за которым следует поворот влево, либо из поворота влево, за которым следует поворот вправо, причем конечным результатом обеих операций является повышение ранга узла на два уровня. И напротив, операции спаренного одностороннего поворота состоят из двух выполняемых последовательно поворотов вправо или влево. Цель выполнения всех этих спаренных операций состоит в повышении ранга узла на два уровня.

На рис. 8.4 показана операция спаренного двустороннего поворота, которая начинается с поворота влево вокруг узла P. В результате ранг узла R повышается, а ранг узла P понижается. На следующем шаге выполняется вращение вправо вокруг узла G, в результате которого ранг узла R снова повышается, а ранг узла G понижается. Общим результатом операции спаренного двустороннего поворота будет локальная балансировка дерева.

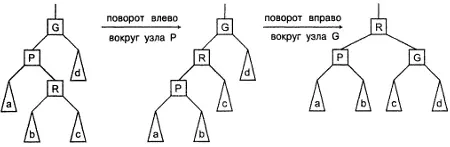
Рисунок 8.4. Операция спаренного двустороннего поворота

На рис. 8.5 изображены обе операции спаренного одностороннего поворота, поскольку они дополняют друг друга. Обратите взимание, что операция спаренного одностороннего поворота всегда начинается с поворота вокруг верхнего узла.

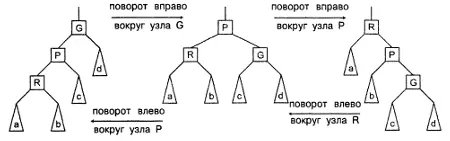
Рисунок 8.5. Операция спаренного одностороннего поворота

Как бы то ни было, ознакомившись с этими операциями простых и спаренных двухсторонних и односторонних поворотов, мы может их использовать в структуре данных, называемой скошенным деревом. Скошенное дерево (splay tree) - это дерево бинарного поиска, сконструированное таким образом, что любое обращение к узлу приводит к его скосу в сторону корневого узла. Скос заключается в применении операций спаренного двустороннего или одностороннего поворота до тех пор, пока скашиваемый узел не окажется в позиции корневого узла дерева или на один уровень ниже него. В последнем случае его ранг можно повысить до корневого узла, выполнив одиночный поворот. Концепция скошенного дерева была изобретена Д. Д. Слеатором (D. D. Sleator) и Р. Е. Таръяном (R. E. Tarjan) в 1985 году [22].

Вначале рассмотрим операцию поиска, т.е. нахождение конкретного узла. Мы начнем с применения стандартного алгоритма поиска в дереве бинарного поиска. Обнаружив искомый узел, мы выполняем его скос к корневому узлу.

Иначе говоря, мы применяем операции спаренного двустороннего либо одностороннего поворота, перемещая узел вверх по дереву до тех пор, пока он не достигнет позиции корневого узла. Если в результате этих операций узел оказывается на втором уровне, мы больше не можем применять операции спаренного поворота, и поэтому для перемещения в позицию корневого узла применяем поворот влево или вправо.

Если поиск был безрезультатным, в ходе него мы должны натолкнуться на нулевой узел. В этом случае мы выполняем скос узла, который был бы родительским узлом, если бы искомый узел существовал. Естественно, при этом следовало бы сообщить о невозможности как-либо найти элемент.

Вставку также легко описать: необходимо применить обычный алгоритм вставки в дерево бинарного поиска, а затем выполнить скос добавленного узла.

Чтобы выполнить удаление, мы выполняем обычное удаление из дерева бинарного поиска, а затем выполняем скос родительского узла того узла, который был удален.