Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Вначале предположим, что узел и является черным. Для достижения поставленной цели достаточно выполнить либо одиночный поворот, либо спаренный двусторонний поворот, а затем перекрасить некоторые узлы. В первом случае, который на рис. 8.8 представлен первым преобразованием, мы выполняем поворот узла d вправо на место узла g, чтобы g стал дочерним узлом узла d. Затем мы перекрашиваем узел d в черный цвет, a g - в красный. Во втором случае (нижнее преобразование на рис. 8.8) мы выполняем спаренный двусторонний поворот, чтобы поместить узел s на место g, а затем перекрашиваем узел s в черный цвет, a g - в красный. Обратите внимание, что абсолютно не важно, является ли узел и внешним или внутренним; достаточно, чтобы он был черным.

Естественно, возможны еще два случая, представляющие собой зеркальное отражение рассмотренных, однако мы не будем их рассматривать. На рисунке 8.8 легко видеть, что теперь условие, определенное для красных узлов, удовлетворено, и что операции поворота и перекрашивания не нарушают условие, определенное для черных узлов.

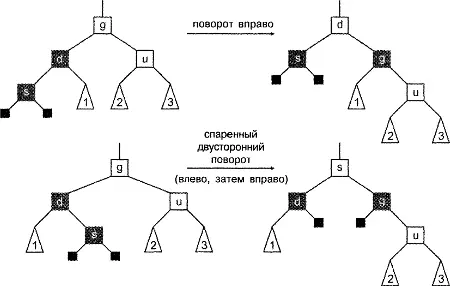
Рисунок 8.8. Балансировка после вставки: два простых случая

Этот случай был простым. Теперь рассмотрим более сложный. Предположим, что узел и, дядя нового узла, также окрашен в красный цвет. Первый шаг прост: мы перекрашиваем узлы d и u в черный цвет, а g в красный. Условие для черных узлов по-прежнему выполняется, но, похоже, мы ухудшили общую ситуацию, поскольку условие, определенное для красных узлов, перестало выполняться. Вместо того чтобы признать, что узел s нарушает условие, определенное для красных узлов, мы предположили, каким мог бы быть узел g. В конце концов, родительский узел узла g мог бы быть и красным. Иначе говоря, в действительности эта операция перекрашивания не решает никаких проблем. Мы просто отложили решение проблемы на неопределенный срок. Но действительно ли ситуация ухудшилась? Посмотрите, что мы сделали: мы переместили проблемный узел вверх по дереву. Перемещение вверх ограничено в пространстве, поскольку со временем мы натолкнемся на корневой узел.

Итак, перенесем свое внимание двумя уровнями выше, примем, что узел g является новым узлом и посмотрим, нарушили ли мы какие-либо правила. Иначе говоря, снова применим рассмотренный алгоритм, но на этот раз начнем рассмотрение с узла g. Два возможных случая показаны на рис. 8.9 (естественно, могут существовать и два случая, являющиеся зеркальными отражениями представленных, но они не показаны). В обоих результирующих деревьях узел g помечен тремя восклицательными знаками, указывающими, что он может нарушать одно из двух правил, и что необходимо продолжать процесс, снова повторяя действия алгоритма.

Не прибегая к подробным математическим выкладкам, отметим, что подобно случаю применения простого бинарного дерева, алгоритм вставки в красно-черное дерево является алгоритмом типа O(log(n)), хотя в этом случае постоянный коэффициент имеет большее значение, поскольку приходится учитывать возможные повороты и повышение ранга узлов.

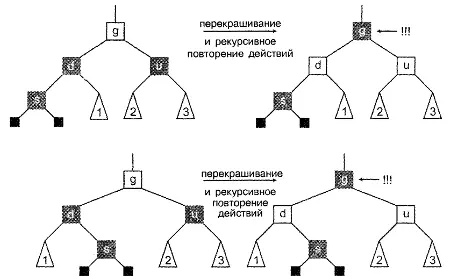
Рисунок 8.9. Балансировка после вставки: два рекурсивных случая

Код реализации этого алгоритма вставки и балансировки приведен в листинге 8.23. Метод содержит внутренний цикл, выход из которого выполняется, когда баланс дерева восстановлен. В начале цикла предполагается, что балансировка дерева должна быть выполнена в данном цикле, и что перемещение по дереву вверх должно выполняться только в том случае, если мы уверены, что снова будем выполнять цикл. В остальном приведенный код служит достаточно точным представлением алгоритма вставки в красно-черное дерево. Единственный неприятный момент - необходимость поддержания информации о том, являются ли определенные узлы левыми или правыми дочерними узлами своих родительских узлов.

Листинг 8.23. Вставка в красно-черное дерево

procedure TtdRedBlackTree.Insert(aItem : pointer);

var

Node : PtdBinTreeNode;

Dad : PtdBinTreeNode;

Grandad : PtdBinTreeNode;

Uncle : PtdBinTreeNode;

OurType : TtdChildType;

DadsType : TtdChildType;

IsBalanced : boolean;

begin

{вставить новый элемент, вернуться к вставленному узлу и его связям с родительским узлом}

Node := bstInsertPrim(aItem, OurType);

{окрасить его в красный цвет}

Node^.btColor := rbRed;

{продолжать применение в цикле алгоритмов балансировки при вставке в красно-черное дерево до тех пор, пока дерево не окажется сбалансированным}

repeat

{предположим, что дерево сбалансировано}

IsBalanced :=true;

{если узел является корневым, задача выполнена и дерево сбалансировано, поэтому будем считать, что мы находимся не в корневом узле}

if (Node <> FBinTree.Root) then begin

{поскольку мы находимся не в корневом узле, необходимо получить родительский узел данного узла}

Dad := Node^.btParent;

{если родительский узел черный, задача выполнена и дерево сбалансировано, поэтому будем считать, что родительский узел красный}

if (Dad^.btColor = rbRed) then begin

{если родительский узел является корневым, достаточно перекрасить его в черный цвет, и задача будет выполнена}

if (Dad = FBinTree.Root) then

Dad^.btColor := rbBlack {в противном случае родительский узел, в свою очередь, имеет родительский узел}

else begin

{получить прародительский узел (он должен быть черным) и перекрасить его в красный цвет}

Grandad := Dad^.btParent;

Grandad^.btColor := rbRed;

{получить узел, соответствующий понятию дяди}

if (Grandad^.btChild[ctLeft] = Dad) then begin

DadsType := ctLeft;

Uncle := Grandad^.btChild[ ctRight ];

end

else begin

DadsType := ctRight;

Uncle := Grandad^.btChild[ ctLeft ];

end;

{если дядя тоже имеет красный цвет (обратите внимание, что он может быть нулевым!), окрасить родительский узел в черный цвет, дядю в черный цвет и повторить процесс, начиная с прародительского узла}

if IsRed(Uncle) then begin

Dad^.btColor :=rbBlack;

Uncle^.btColor := rbBlack;

Node := Grandad;

IsBalanced := false;

end

{в противном случае дядя окрашен в черный цвет?}

else begin

{если текущий узел имеет такие же отношения со своим родительским узлом, какие его родительский узел имеет с прародительским (т.е. они оба являются либо левыми, либо правыми дочерними узлами), нужно окрасить родительский узел в черный цвет и повысить его ранг. Задача выполнена}

OurType := GetChildType(Node);

if (OurType = DadsType) then begin

Dad^.btColor := rbBlack;

rbtPromote(Dad);

end

{в противном случае необходимо окрасить узел в черный цвет и повысить его ранг посредством применения спаренного двустороннего поворота; задача выполнена}

else begin

Node^.btColor :=rbBlack;

rbtPromote(rbtPromote(Node));

end;

end;

end;

end;

end;

until IsBalanced;

end;

Необходимо принимать во внимание один небольшой нюанс: следует проверять цвета узлов. Некоторые из узлов, которые мы будем проверять, будут внешними, т.е. нулевыми. Для повышения читабельности кода я написал небольшую подпрограмму IsRed, которая выполняет проверку на наличие нулевого узла (возвращая значение false), прежде чем выполнять проверку поля цвета узла.