Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Вначале необходимо рассмотреть случай, когда нарушающий узел имеет черный родительский узел и два черных узла-племянника. Перекрашивание братского узла в красный цвет приводит к перемещению проблемной области вверх к родительскому узлу, и можно просто повторить весь алгоритм применительно к этому узлу, как к нарушающему правило. Эта возможность показана на рис. 8.12.

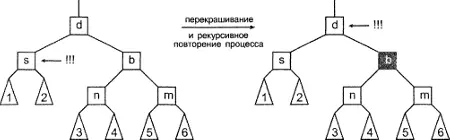
Рисунок 8.12. Балансировка после удаления: первый случай

Второй возможный случай - существование красного родительского узла и двух черных узлов-племянников. Этот случай даже проще предыдущего: нужно перекрасить родительский узел в черный цвет, а братский - в красный. Путь, проходящий через нарушающий узел, снова имеет требуемое количество черных узлов (тем самым удовлетворяя правило 2). Это же можно сказать и по поводу пути, проходящего через братский узел (правило 2 снова выполняется). Только что окрашенный в красный цвет узел имеет черный родительский узел, следовательно, правило 3 не нарушается. Стало быть, мы снова получаем красно-черное дерево. Этот случай показан на рис. 8.13.

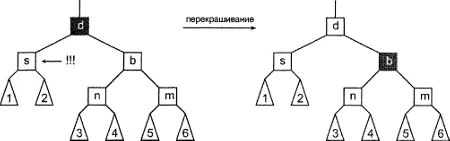
Рисунок 8.13. Балансировка после удаления: второй случай

Теперь предположим, что противоположный по отношению к нарушающему узлу узел-племянник является красным. (Иначе говоря, если нарушающий узел -это левый дочерний узел родительского узла, речь идет о правом узле-племяннике, а если нарушающий узел - правый дочерний узел, речь идет о левом узле-племяннике.) Перекрасим этот узел-племянник в черный цвет. Окрасим братский узел в цвет родительского узла (первоначальный цвет родительского узла не имеет значения), а родительский узел - в черный цвет. Затем повернем родительский узел и повысим ранг братского узла. Тщательно проанализируем эту ситуацию, глядя на рис. 8.14. Вначале проверим выполнение правила 3: очевидно, что мы не ввели никаких новых красных узлов, следовательно, можно быть уверенным, что это правило выполняется. Теперь рассмотрим выполнение правила 2. Все пути, проходящие через нарушающий узел, содержат дополнительный черный узел, что ведет к устранению проблемы, возникшей в результате удаления исходного узла. Все пути, проходящие через дочерние деревья 5 и 6, также содержат то же количество черных узлов, что и ранее. Следовательно, во всех случаях правило 2 выполняется, и результирующее дерево снова является красно-черным.

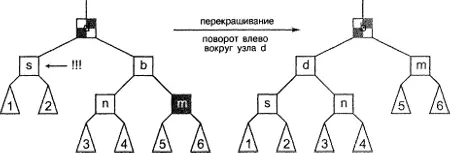
Рисунок 8.14. Балансировка после удаления: третий случай

Теперь рассмотрим последний случай. Предположим, что противоположный узел-племянник окрашен в черный цвет, но второй узел этой же степени родства является красным. На этот раз нужно выполнить спаренный двусторонний поворот. Вначале мы окрашиваем узел-племянник в цвет родительского узла (как и в предыдущем случае, первоначальный цвет родительского узла значения не имеет), а затем перекрашиваем родительский узел в черный цвет. Далее мы поворачиваем братский узел, чтобы повысить ранг узла-племянника, а затем поворачиваем родительский узел, чтобы снова повысить ранг узла-племянника. Это преобразование показано на рис. 8.15. В любом случае это не ведет к непреднамеренному нарушению правила 3: мы не ввели никаких новых красных узлов. Теперь что касается правила 2 - все пути, проходящие через нарушающий узел, содержат один дополнительный черный узел, следовательно, ранее описанная проблема устранена. Все пути, проходящие через дочернее дерево 3, по-прежнему содержат одинаковое количество черных узлов. Аналогично, во всех путях, проходящих через дочерние деревья 4, 5 и 6, не был вставлен или удален какой-либо дополнительный черный узел, следовательно, правило 3 по-прежнему выполняется. Дерево снова оказывается красно-черным.

Если нарушающий узел удается переместить до позиции корневого узла, создается предельная ситуация. В этом случае нарушающий узел не имеет родительского узла и, следовательно, не может иметь братский узел. При этом нарушающий узел больше не представляет проблемы.

Конечно, все рассмотренные случаи имеют аналоги, представляющие их зеркальные отражения, но при этом анализ каждого из случаев удаления остается тем же. При написании кода подпрограммы удаления нужно будет убедиться, что мы правильно отразили как левые, так и правые варианты расположения узлов.

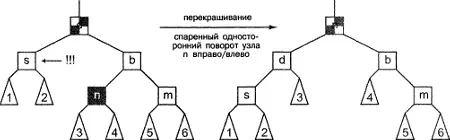
Рисунок 8.15. Балансировка после удаления: заключительный случай

Итак, мы рассмотрели все возможности. При этом использовались два рекурсивных шага или, точнее, два шага, которые требовали дальнейших усилий по балансировке. Первый - когда братский узел был красным, и его нужно было сделать черным. Второй - когда родительский, братский и узлы-племянники были черными. Существовали еще три случая: родительский узел был красным, а братский узел и узлы-племянники были черными;

братский узел был черным, а дальний узел-племянник красным (цвет родительского узла и ближайшего узла-племянника "не имели значения");

и, наконец, случай, когда братский узел был черным, дальний узел-племянник черным, а ближайший узел-племянник красным. Если вы еще раз взглянете на рисунки 8.12, 8.13, 8.14 и 8.15, то убедитесь, что мы рассмотрели все варианты.

Опуская математические выкладки, отметим, что алгоритм удаления из красно-черного дерева является алгоритмом типа O(log(n)), хотя постоянный коэффициент времени больше, чем в случае простого бинарного дерева.

Операция удаления узла из красно-черного дерева реализуется с помощью кода, представленного в листинге 8.25.

Листинг 8.25. Удаление из красно-черного дерева

procedure TtdRedBlackTree.Delete(aItem : pointer);

var

Node : PtdBinTreeNode;

Dad : PtdBinTreeNode;

Child : PtdBinTreeNode;

Brother : PtdBinTreeNode;

FarNephew : PtdBinTreeNode;

NearNephew : PtdBinTreeNode;

IsBalanced : boolean;

ChildType : TtdChildType;

begin

{выполнить поиск узла, который нужно удалить; этот узел будет иметь единственный дочерний узел}

Node := bstFindNodeToDelete(aItem);

{если узел красный или является корневым, его можно безнаказанно удалить}

if (Node^.btColor = rbRed) or (Node = FBinTree.Root) then begin

FBinTree.Delete(Node);

dec(FCount);

Exit;

end;

{если единственный дочерний узел является красным, перекрасить его в черный цвет и удалить узел}

if (Node^.btChild[ctLeft] =nil) then

Child := Node^.btChild[ctRight] else

Child :=Node^.btChild[ctLeft];

if IsRed(Child) then begin

Child^.btColor :=rbBlack;

FBinTree.Delete(Node);

dec(FCount);

Exit;

end;

{на этом этапе узел, который нужно удалить, - узел Node; он является черным и известно, что дочерний узел Child, который его заменит, является черным (а также может быть нулевым!) и что существует родительский узел узла Node (который вскоре станет родительским узлом узла Child); братский узел узла Node также существует в соответствии с правилом, сформулированным для черных узлов}