Михаил Краснов - Графика DirectX в Delphi

Поменять схему окрашивания или тонирования примитивов возможно с помощью знакомого уже метода задания режимов воспроизведения. Например, чтобы отказаться от интерполяции цветов, надо записать следующую строку:

FD3DDevice.SetRenderState(D3DRS_SHADEMODE, D3DSHADE_FIAT);

В этом случае цвет первой вершины треугольника будет определять цвет всего примитива.

Вторым аргументом для указанного режима могут использоваться также константы D3DSHADE_COURAUD и D3DSHADE_PHONG. Второй случай пока аналогичен отказу от интерполяции.Еще одним режимом воспроизведения, на который необходимо обязательно обратить внимание, является режим D3DRS_FiLLMODE. По умолчанию действует твердотельный режим, примитивы выводятся заполненными. Этому режиму соответствует константа DSDFILL^SOLID. Для установления проволочного, каркасного режима воспроизведения необходимо вторым аргументом метода setRenderState задавать другую константу:

FD3DDevice.SetRenderState(D3DRS_FILLMODE, D3DFILL_WIREFRAME);

При проволочном режиме вложенные в треугольник объекты не воспроизводятся, рисуются только отрезки, образующие их контуры. Иллюстрацией применения этого метода служит проект каталога Ех24 - простое продолжение примера со звездой (рис. 7.14).

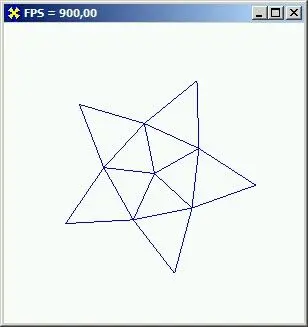
Если для этого режима использовать константу D3DFiLL_POiNT, то при воспроизведении станут выводиться только точки вершин примитивов.

Продолжаем изучать примитивы DirectSD. Группе связанных треугольников соответствует флаг DSDPTJTRIANGLESTRIP. Первые три вершины задают первый треугольник, вторая, третья и четвертая определяют второй треугольник, третья, четвертая и пятая - третий и т. д. Получается лента соприкасающихся треугольников (рис. 7.15).

Использование связанных треугольников - самый экономный и эффективный способ построений. К примеру, если для рисования прямоугольника независимыми треугольниками потребуется задать координаты шести точек, то при использовании связанных треугольников достаточно задать четыре точки.

Для закрепления изученного материала решим следующую задачу: требуется нарисовать диск; значение константы Level определяет количество используемых в разбиении треугольников.

Поскольку лента в этой задаче замкнута, вершин потребуется на пару больше, чем значение Level:

VPoints : Array [0..Level + 1] of TCUSTOMVERTEX;

Для построения диска берем попарно точки, лежащие на внутренней и внешней границах диска:

i := 0;

repeat

with VPoints [i] do begin // Внутренняя граница диска

X := 150 + cos (Angle + i * 2 * Pi / Level) * Radius / 2;

Y := 150 + sin (Angle + i * 2 * Pi / Level) * Radius / 2;

Color := D3DCOLOR_XRGB(255, 0, 0); // Красного цвета

end;

with VPoints [i + 1] do begin // Внешняя граница диска

X := 150 + cos (Angle + i * 2 * Pi / Level) * Radius;

Y := 150 + sin (Angle + i * 2 * Pi / Level) * Radius;

Color := D3DCOLOR_XRGB(0, 0, 255); // Синего цвета

end;

Inc (i, 2); // Переходим к следующей паре вершин

until i > Level;

Окончательное решение задачи можете посмотреть в каталоге Ех25, результат работы которого в проволочном режиме представлен на рис. 7.16.

Раз мы умеем строить закрашенный прямоугольник, то мы можем попробовать свои силы в решении классической задачи компьютерной графики - рисование пламени. Проект, располагающийся в каталоге Ех26, является решением этой задачи, во время его работы внизу экрана поднимаются языми пламени, в верхней части экрана появляется падающая горящая частица.

Изображение строится по отдельным квадратикам, размеры которых можно варьировать:

type

TRGB = packed record // Запись цвета

R, G, В : BYTE;

end;

const

Size =2; // Размер отдельного квадратика, "пиксела"

Fade =4; // Степень затухания пламени

NumX = 150; // Количество квадратиков по горизонтали

NumY = 150; // Количество квадратиков по вертикали

var

Fire : Array [L.NumX, L.NumY + 1] of TRGB; // Цвета узлов сетки

PreF : Array [L.NumX] of TP.GB; // Вспомогательный массив первой строки

Angle : Single = 0.0; // для движения падающей точки

ParticleX : Integer =0; // Координаты точки

ParticleY : Integer = NumY;

Следующая пользовательская функция выводит один квадрат, цвета углов которого задаются текущими значениями элементов массива Fire:

function TfrmDSD.DrawPix(const inX, inY : Integer) : HRESULT;

var

pVertices : PByte;

hRet : HRESULT;

begin

with VPoints [0] do begin // Левый нижний угол квадрата

X := inX * Size;

Y := 300 - inY * Size; // Переворачиваем ось Y

Color := D3DCOLOR_XRGB(Fire[inX, inY + 1].R, Fire[inX, inY + 1].G,

Fire[inX, inY + 1].B);

end;

with VPoints [1] do begin // Левый верхний угол квадрата

X := inX * Size;

Y := 300 - (inY + 1) * Size;

Color := D3DCOLOR_XRGB(Fire[inX, inY].R, Fire[inX, inY].G,

Fire[inX, inY].B); end; with VPoints [2] do begin // Правый нижний угол квадрата

X := (inX + 1) * Size;

Y := 300 - inY * Size;

Color := D3DCOLOR_XRGB(Fire[inX + 1, inY + 1].R, Fire[inX + 1,

inY + 1].G, Fire[inX + 1, inY + 1].B);

end;

with VPoints [3] do begin // Правый верхний угол квадрата

X := (inX + 1) * Size;

Y := 300 - (inY + 1) * Size;

Color := D3DCOLOR_XRGB(Fire[inX + 1, inY].R, Fire[inX + 1, inY].G,

Fire[inX + 1, inY].B);

end;

hRet := FD3DVB.Lock(0, SizeOf(VPoints), pVertices, 0];

if Failed (hRet) then begin

Result := hRet;

Exit;

end;

Move (VPoints, pVertices^, SizeOf(VPoints));

hRet := FD3DVB.Unlock;

if FAILED(hRet) then begin

Result := hRet;

Exit;

end;

Result := FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 2);

end;

Для формирования собственно пламени последняя строка инициализируется случайным оттенком красного, в последующих пикселах цвет затухает, а для создания эффекта размытия языков пламени используется простой прием с усреднением цветов соседних точек:

procedure TfrmD3D.DrawFire;

i, j : Integer;

f : Byte;

begin

// Инициализация последней строки экрана

for i := 2 to NumX-1 do begin

f := random(255) ;

PreF[i].R := 255;

PreF[i].G := trunc (f / 1.4);

PreF[i] . := f div 2;

end;

// Заполняем в массиве Fire последнюю строку

// усредненными значениями соседних элементов

PreF '" for i := 2 to NumX - 1 do begin

Fire[i, 1}.R := (PreF[i - 1] .R 4- PreF[i 4- 1} .R + PreF[i] .R) div 3; $; Fire[i, 1].G := (PreF[i - 1] .G + PreF[i + 1] .G + PreF[i] .G) div 3; Fire[i, 1].B := (PreF[i - 1].B + PreF[i + 1].B + PreF[i].B) div 3; end;

// Смешивание, усреднение значений пикселов по экрану for j := NumY - 1 downto 2 do for i := 2 to NumX - 1 do begin

Fire[i,j].R := (Fire[i-1, j].R + Fire[i+1, j].R + Fire[i,j].R +

Fire[i-1, j-1].R + Fire[i+1, j-1].R +

Fire[i, j-1].R) div 6;

Fire[i,j].G := (Fire[i-1, j].G + Fire[i+1, j].G + Fire[i,j].G +

Fire[i-1, j-1].G + Fire[i+l, j-1].G +

Fire[i, j-1].G) div 6;

Fire[i,j].B := (Fire[i-1, j].B + Fire[i+1, j].B +

Fire[i,j].B + Fire[i-1, j-1].B + Fire[i+1, j-1].B +

Fire[i, j-1].B) div 6;

end;

// Квадратик, соответствующий падающей частице for j := ParticleY - 1 to ParticleY do

for j := ParticleX - 1 to

ParticleX do begin

Fire[i, j].R := 255;

Firefi, j].G := 0;

Fire[i, j].B := 0;

end;

// Вывод квадратиков содержимого экрана

for j := 2 to NumY - 1 do

for i := 2 to NumX - 1 do

DrawPix (i - 1, j - 1) ;

// Затухание оттенков по мере подъема языков пламени

for j := NumY downto 2 do

for i := 1 to NumX do begin

if Fire[i, j - 1J.R >= Fade

then Firefi, j].R = Firefi, j - 1].R- Fade

else Firefi, j].R = 0;

if Firefi, j - 1].G >= Fade

then Firefi, j].G = Firefi, j - 1].G - Fade

else Firefi, j].G = 0;

if Firefi, j - 1].B >= Fade

then Firefi, j].B = Firefi, j - 1].B - Fade