Михаил Краснов - Графика DirectX в Delphi

Точечный источник света также подходит для освещения объектов, покрытых текстурой. Так, в примере проекта каталога Ех16 рисуется тестовая сцена комнаты с конусом и сферой. На стены комнаты здесь накладываются разнообразные текстуры.

В предыдущих примерах текстура накладывалась на простые объекты, но вам, наверняка, захочется узнать, возможно ли использование текстуры с объектами сложной формы. Если у вас возникли вопросы по этому поводу, отсылаю вас к следующему примеру, проектам каталога Ех17, в одном из которых выводится модель игрока из игры Quake, а во втором - вращающаяся голова. Программа импорта, которой я пользовался для подготовки примеров этой книги, позволяет записывать в результирующем файле и текстурные координаты моделей. Мне оставалось только отметить такую опцию при записи результирующего файла.

Механизм трехмерной игры

Этот раздел я закончу примером, который можно считать заготовкой трехмерной игры. Но прежде, чем мы перейдем непосредственно к этому проекту, посмотрим решение двух связанных с ним задач: вывод текста в пространстве и раскрашивание модели.

Вам, наверняка, пригодится моя простая программа из каталога Ех18, с помощью которой создается файл, содержащий координаты вершин треугольников, образующих нужный символ установленного для формы шрифта. Программа основана на материале моей книги по OpenGL, подробно рассматривать ее здесь не буду, ограничусь лишь небольшими замечаниями по поводу ее использования.

Требуемый символ должен устанавливаться аргументом процедуры OutText, вызываемой в коде два раза: первый раз - для получения координат вершин треугольников, второй раз - для контрольного отображения на экране. В текстовый файл выводятся построчно две координаты очередной вершины треугольника, по оси X и по оси Y. Количество треугольников заранее неизвестно и зависит от базового символа. Выводимые в файл координаты вершин соответствуют оконным, поэтому при дальнейшем использовании должны быть масштабированы. Как правило, вершины треугольников перечисляются по часовой стрелке, но возможны исключения.

Еще один проект (из каталога Ех19) строит средствами Direct3D символ, используя файл, полученный по результатам работы предыдущей программы. Количество считываемых треугольников необходимо установить равным константе NumTriangies. Считываемые координаты вершин масштабируются при заполнении буфера вершин.

Замечу также, что оба примера могут использоваться и для вывода фраз целиком, а не только отдельных символов.

Сейчас перейдем к очередному примеру (проекту из катаюга Ех20), во время работы которого на экране воспроизводится симпатичная модель человечка из детского конструктора (рис. 10.11).

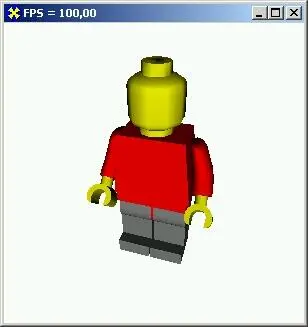
Подходящую модель я нашел по Internet-адресу http://www.people.zeelandnet.nl /nihil/download/legoman.zip. Автор модели, Kortekaas, любезно предоставил разрешение на использование ее в этой книге.

Эта модель также конвертирована мною с помощью программы импорта 3D Exploration, а код был преобразован из программы на языке C++. При импортировании комплексных моделей, состоящих, как в данном примере, из нескольких частей, в код вставляются метки-имена составляющих элементов. По этим меткам можно ориентироваться для получения данных о том, сколько треугольников потрачено на описание отдельной части, чтобы идентифицировать каждый элемент:

procedure TfrmD3D.DrawScene;

begin

with FD3DDevice do begin

// Ноги покрашены материалом серого цвета

SetMaterial(MaterialGray);

SetTransform(D3DTS_WORLD, matLeftFoot);

// Левая нога

DrawPrimitive(D3DPT_TRIANGLELIST, 0, 112);

// Правая нога

SetTransform(D3DTS_WORLD, matRightFoot) ;

DrawPrimitive(D3DPT TRIANGLELIST, (112 + 204) * 3, 112);

// Руки покрашены красным цветом SetMaterial(MaterialRed) ; // Левая рука

SetTransform(D3DTS_WORLD, matLeftHand);

DrawPrimitive(D3DPT_TRIANGLELIST, (112+204 + 112 + 620 + 6141*3, 612); // Кисти - желтого цвета

SetMaterial(MaterialYellow) ; // Левая кисть

DrawPrimitive(D3DPT_TRIANGLELIST,(112+204+112+620+614+612)*3, 324);

SetMaterial(MaterialRed); SetTransform(D3DTS_WORLD, matRightHand); // Правая рука

DrawPrimitive(D3DPTJTRIANGLELIST, (112 + 204 + 112 + 620) * 3, 614); // Правая кисть

SetMaterial(MaterialYellow) ;

DrawPrimitive(D3DPT_TRIANGLELIST,

(112+204+112+620+614+612+324)*3, 324); // Голова

S.etTransform(D3DTS_WORLD, matRot) ;

DrawPrimitive(D3DPTJTRIANGLELIST, (112 + 204 + 112) * 3, 620); // Туловище, красного цвета

SetMaterial(MaterialRed) ;

DrawPrimitive(D3DPTJTRIANGLELIST, 112 * 3, 204);

end;

end;

Буфер вершин заполняется данными на всю модель целиком, а при воспроизведении отдельных частей из него последовательно выбираются соответствующие треугольники. Перед воспроизведением каждого элемента устанавливается предварительно рассчитанная матрица трансформаций, поэтому изначально монолитная модель пришла в движение. Для каждого элемента модели задается индивидуальный материал, поэтому модель стала разноцветной. Фигурирующие числа получены следующим образом: я подсчитал количество отдельных фасетов между метками, расставленными программой моделирования трехмерных объектов в описании массива face^indicies.

Матрицы, связанные с поворотом конечностей, из соображений оптимизации вычисляются не при каждой перерисовке кадра, а только при изменении значений управляющих переменных. Обратите внимание, что поворот конечностей в точках крепления осуществляется следующим образом: система координат перемещается в точку крепления, выполняется поворот, а затем система координат возвращается в первоначальное положение:

procedure TfrmDSD.MoveMan;

begin

// Поворот глобальной системы координат,

// вращение всей модели вокруг своей оси

SetRotateZMatrix (matRot, Angle);

// Переменная, задающая вращение конечностей

AngleFoot := AngleFoot + StepFoot;

if (AngleFoot > Pi / 4) or (AngleFoot < -Pi / 4}

then StepFoot := -StepFoot; // Ноги вращаются в противофазе

SetRotateXMatrix (rotLeftFoot, AngleFoot);

SetRotateXMatrix (rotRightFoot, -AngleFoot); // Поворот левой ноги, в три этапа

matLeftFoot := MatrixMul(matRot,

MatrixMul(transFoot2, MatrixMul(rotLeftFoot, transFootl))); // Поворот правой ноги

matRightFoot := MatrixMul(matRot,

MatrixMul(transFoot2,

MatrixMul(rotRightFoot, transFootl))); // Поворот левой руки

matLeftHand := MatrixMul(matRot,

MatrixMul(transHand2,

MatrixMul(rotRightFoot, transHandl))); // Поворот правой руки

matRightHand := MatrixMul(matRot,

MatrixMul(transHand2, MatrixMul(rotLeftFoot, transHandl)));

end;

Рабочие матрицы, связанные с перемещениями в точки крепления конечностей, инициализируются один раз, в начале работы приложения:

SetTranslateMatrix(transFootl, О, О, 0.25);

SetTranslateMatrix(transFoot2, О, О, -0.25);

SetTranslateMatrix(transHandl, 0.25, 0.0, -0.23);

SetTranslateMatrix(transHand2, -0.25, 0.0, 0.23);

Этот пример я подготовил для использования в дальнейшем в расчете на то, что человечком можно будет легко управлять, перемещая его в пространстве. Но если на сцене присутствует только одна модель, для оптимизации можно сократить количество операций с матрицами. В самом деле, в этом примере матрица matRot, связанная с глобальной системой координат, может вообще не использоваться: модель можно не вращать и оставить неподвижной, а перемещать точку зрения наблюдателя. Эффект вращения модели останется, а количество операций существенно уменьшится.