Алексей Цвелик - Жизнь в невозможном мире: Краткий курс физики для лириков

Чтобы обсуждение не выглядело совершенно отвлеченно, приведу пример применения комплексных чисел. Вот, скажем, нам надо посчитать площадь под кривой, заданной уравнением у = 1/(х 2+ 1), часть которой изображена на рисунке (предполагается, что кривая простирается от минус до плюс бесконечности, но этого, понятно, не нарисуешь).

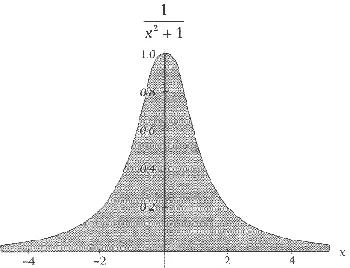
Математически эта задача эквивалентна вычислению интеграла:

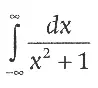
Все числа и функции здесь действительные, что очевидно хотя бы из того, что площадь под кривой (закрашена на рисунке серым цветом) действительна. Однако оказывается, что интеграл очень просто вычисляется, если переопределить его как интеграл от комплексной функции. Он равен π = 3,14159… Разумеется, я привел самый простой пример; в данном случае интеграл можно посчитать и без комплексных чисел, но есть множество примеров, когда этого сделать нельзя.

На мнимых числах расширение понятия числа не остановилось. В начале XIX века были введены кватернионы, перешедшие в физику сто лет спустя. В конце XIX века появились так называемые Грассмановы числа, названные так по имени открывшего их немецкого математика Германа Грассмана. Представьте себе объекты, которые можно перемножать (но не делить друг на друга) и складывать, а также интегрировать. Отличие этих объектов от обычных чисел состоит в том, что произведение двух Грассмановых чисел ab меняет знак, когда сомножители меняются местами: ba = — ab. Соответственно, произведение любого Грассманова числа на себя равно нулю. Звучит как игра абстрактного ума, не правда ли? Оказалось (через сто лет), что квантовая теория поля без таких чисел не может обойтись.

А не вспомнить ли историю геометрии Лобачевского? Задал человек себе вопрос: можно ли построить логически непротиворечивую геометрию, отказавшись от постулата о том, что параллельные прямые никогда не пересекаются. Выяснилось, можно. Казалось бы, чистая абстракция. Практики (типа Чернышевского) говорили, что Лобачевский просто сумасшедший. А потом еще более сумасшедший немецкий математик Риман построил общую теорию таких геометрий, куда геометрия Лобачевского вошла как частный случай. А через несколько десятков лет Альберт Эйнштейн воспользовался этими «праздными измышлениями» для создания общей теории относительности, теории непревзойденной красоты и изящества.

Итак, математика, являясь абстрактной и отвлеченной наукой, самым неожиданным образом приносит вполне конкретные плоды. Однако на этом чудеса не кончаются. Давайте зададим себе вопрос: где находятся те объекты, которые математика изучает? Даже самая прикладная математика не имеет дела непосредственно с вещами и явлениями этого мира. Вместо этого она имеет дело с какими-то моделями, идеализациями типа идеальной сферы или окружности. В природе ничего такого совершенного нет (как говорил Гегель, «природа бессильна следовать идее»). Все утверждения математики касаются таких вот идеальных объектов. Например, доказал Пифагор теорему о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы — но где эти треугольники? А вот еще вопрос: выдумал Пифагор эту теорему или открыл? Если бы никто к настоящему времени не доказал этой теоремы, была бы она верна? Или: если все математики когда-нибудь исчезнут, останется ли верной теорема Пифагора? Ясно поэтому, что мир математики принадлежит к миру идей — разумных нематериальных сущностей, существующих объективно, вне нашего желания и воли.

Еще немного о числах. Как для пифагорейцев, так и для многих других мыслителей, мистиков и философов, числа не представляли из себя какой-то безразличный ряд, а обладали некой индивидуальностью. Казалось, что некоторые из них обладают особым смыслом. «Кто имеет ум, тот сочти число зверя, ибо это число человеческое; число его шестьсот шестьдесят шесть» (Отк 13, 18). Имеют ли эти представления под собой какую бы то ни было рациональную основу? Ну вот, например, что было бы, если бы у пространства, в котором мы живем, было не три измерения, а больше или меньше? (Я обсужу этот вопрос подробнее в одной из медитаций.) Было бы вот что: в пространстве более чем трех измерений не существовало бы стабильных атомов, так как электрическое поле не могло бы удержать электроны около ядра, а в пространстве с менее чем тремя измерениями атомы были бы настолько стабильны, что их ионизация была бы невозможна и никаких химических реакций не происходило бы. Так что, с одной стороны, — полный распад, а с другой — полный застой. Таким образом, число «три» здесь выступает, как весьма специальное, пограничное. Или, скажем, число «четыре». Это валентность атомов углерода, с такой валентностью они могут образовывать длиннющие цепочки, в которых две связи каждого атома идут на формирование костяка цепочки, а на две оставшиеся можно насаживать, как буквы, другие атомы (водород, кислород, фосфор и т. д.). Получается идеальное хранилище информации: строка и буквы на строке. На этом и стоит вся биология. Это примеры важных (для нас, разумеется) целых чисел. Однако роль некоторых иррациональных чисел представляется мне неизмеримо большей. Вот, например, основание натуральных логарифмов е = 2,721828… или «пи» = 3,14159… встречаются чуть не в каждой физической формуле. Кстати, е представляется в довольно забавном виде, как предел последовательности (1 +1/n) nгде n целое число при n, стремящемся к бесконечности.

В каждом движении мысли находятся люди, доводящие идею до предела, переходящего в абсурд. Так и приведенные выше чудесные свойства математики породили представления о том, что мир может быть описан, так сказать, на кончике пера, что законы его можно извлечь, постулируя несколько аксиом и далее руководствуясь соображениями непротиворечивости. То есть, если аксиомы выбраны правильно, то построить правильную теорию можно, не оглядываясь на эксперимент. Последний, может, и нужен для правильного выбора аксиом, но не более того. Такая точка зрения не является очевидно абсурдной. В истории науки известны примеры, когда теории удивительной сложности строились, исходя из общих соображений и при практически полном отсутствии экспериментальных данных. Примерами являются теория относительности (как специальная, так и общая) и теория античастиц Дирака (Дирак предсказал существование античастиц, построив математически непротиворечивое объединение квантовой механики и теории относительности). Однако надежды такого «математического фундаментализма» были окончательно похоронены австрийским математиком Куртом Геделем, который доказал, что даже такой относительно простой раздел математики, как теория натуральных (то есть целых положительных) чисел, не может быть построен на основании не только конечного, но даже бесконечного, но счетного количества аксиом. То есть какую бы непротиворечивую систему аксиом мы ни брали, всегда найдутся истинные факты, касающиеся натуральных чисел, которые в рамках этой системы не могут быть доказаны. Так как наука о натуральных числах входит как составляющая в любой отдел математики и физики, то теорема Геделя распространяется на все математическое знание. Значит, от мира отгородиться не удается.