Эдвардс Деминг - Выход из кризиса. Новая парадигма управления людьми, системами и процессами

Упражнение 1 . Дано: чаша с красными и белыми бусинами, доля красных – p , доля белых – q (рис. 53).

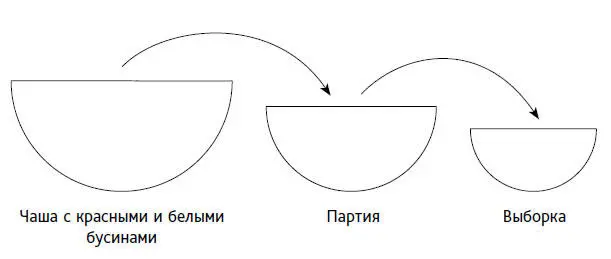
Рис. 53. Партии извлекаются из чаши с красными и белыми бусинами. Затем из партии берется выборка. Замещение каждой бусины, попавшей в партию, обеспечивает постоянство доли p при каждом вынимании

Шаг 1. Извлечем из чаши с помощью случайных чисел с возвратом партию объемом N . Результат:

N всего

X красных

N – X белых

Шаг 2. Извлечем из партии с помощью случайных чисел без возврата выборку объемом n . Результат:

Шаг 3. Вернуть бусины из выборки в партию.

Шаг 4. Повторять шаги 1, 2, 3 неоднократно, сохраняя постоянными объемы партии и выборки. Записать результаты для значений r и s .

Показать, что теоретическое распределение для r и s будет равно:

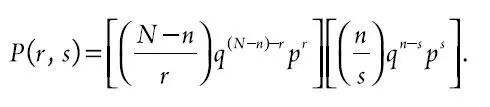(4)

Выводы: а) Число красных бусин в выборке объемом n и число красных бусин в оставшейся части распределены биномиально вокруг одного и того же значения p ; б) независимы друг от друга. То есть число красных бусин в остатке, соответствующем выборкам с количеством дефектных изделий s = 17, будет распределено точно так же, как и число красных бусин в остатке, соответствующем выборкам с s = 0 дефектных изделий.

Эта теорема ужасна. В ней утверждается, что если отдельные дефекты независимы, как это обычно свойственно процессу, находящемуся в статистически хорошо управляемом состоянии, то любая попытка использовать план приемочного контроля для принятия решения о 100 %-ной разбраковке оставшейся части партии будет равносильна подбрасыванию монеты [114]. (Подбрасывание монеты намного дешевле, чем испытания выборок.)

Вместо того чтобы брать выборку из партии, можно просто разделить партию с помощью случайных чисел на две части – выборку и остаток.

Упражнение 2 . Если распределение дефектов в партиях уже, чем биномиальное, и если правило приемки остатка основано на испытаниях выборки, тогда правило будет таким: принимать остаток так, как он есть, когда в выборке много дефектов, и браковать остаток и проводить в нем отбраковку, когда в выборке мало или совсем нет дефектов, т. е. действовать наперекор обычным правилам [115].

Простой способ понять, как получается вышеописанный результат, – рассмотреть ситуацию, когда все входящие партии содержат одно и то же число дефектных изделий. Дефекты, которых нет в остатке, содержатся в выборке, и наоборот. Следовательно, большое число дефектных изделий в выборке будет указывать на малое их число в остатке.

И. Хилл (1960) указал на простой способ производить партии с однородным качеством. Допустим, 20 станков изготавливают одно и то же изделие, 19 из них не производят дефектов, а один выпускает только негодные изделия. Для формирования партии возьмем по одному изделию от каждого из 20 станков. Тогда каждая партия из 20 изделий будет содержать 5 % дефектных изделий.

Партии почти постоянного качества не исключительное явление. Рассмотрим блок фиксирующих поддонов, например, в количестве 12 штук. Они вращаются в процессе штамповки листового металла. Один из поддонов неисправен. Почти все изделия, которые штампуются на нем, окажутся дефектными. Остальные 11 поддонов в хорошем состоянии. Выход партий, формируемых из 12 последовательных изделий, будет постоянно близок к значению 1/12, или 8,3 % дефектных.

Упражнение 3. Доказательство правила «все или ничего» . Выберем с помощью случайных чисел деталь из партии. Назовем ее деталью i . Она может быть дефектной или качественной. Следует ли нам проверить ее или пустить прямо в производство безо всякого контроля? Мы можем представить среднюю полную стоимость в виде таблицы (табл. 5).

Таблица 5

Мы видим, что варианты «да» и «нет» одинаковы, если p = k 1/k 2 . Такое качество Александр Муд назвал равновесным. В точке равновесного качества полная стоимость одинакова для варианта «нет» и варианта «да». Дальше мы видим, что если p < k 1/k 2 , то к меньшим общим потерям приводит вариант «нет», а если p > k 1/k 2 , то вариант «да» (см. рис. 54).

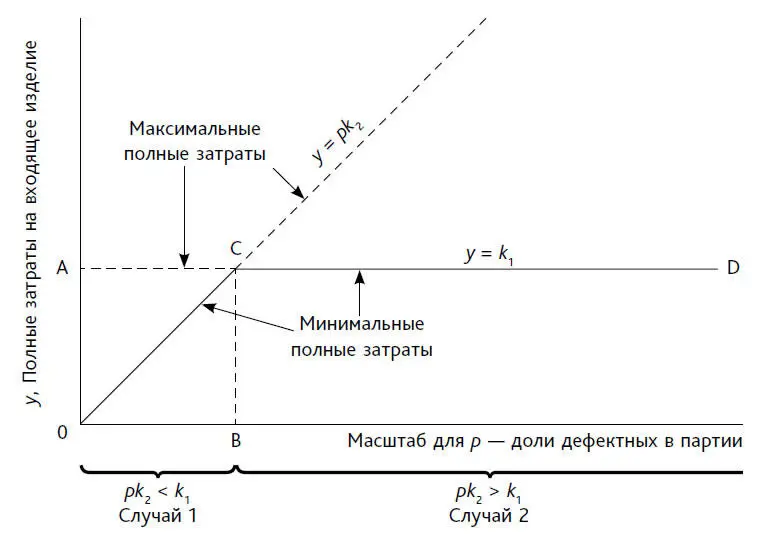
Рис. 54. График, показывающий минимальные полные затраты на изделие в партии в зависимости от входящего качества p . Минимальная доля дефектных изделий лежит вдоль линии 0ВГ. Излом В происходит в точке равновесного качества Б, где p = k 1/k 2 . Полная стоимость максимизируется при использовании 100 %-ного контроля там, где минимум полных затрат обеспечило бы отсутствие контроля, и наоборот

Очевидно, что если наихудшая партия, которая поступит (например) на следующей неделе, будет отстоять слева от точки равновесия, то остальные партии будут лучше, еще больше отдаляясь влево. Ясно, что в этих условиях отсутствие контроля приведет к минимуму средних полных затрат (случай 1).

Если наилучшая партия находится справа от точки равновесия, тогда все другие партии будут хуже и отстоять еще дальше вправо. Это пример случая 2. Полный контроль всех партий приведет к минимуму средних полных затрат.

Таким образом, минимальные средние полные затраты лежат на ломаной линии 0ВГ. Для значений p , близких к точке равновесного качества Б, разницей между отсутствием контроля и 100 %-ным контролем можно пренебречь.

Упражнение 4.Минимальные средние полные затраты для множества деталей [116]. Допустим, мы имеем всего M деталей. Пусть pi – средняя доля дефектных для i-й детали, а k i – стоимость проверки одной детали. Дополнительную стоимость отказа сборки обозначим К , предполагая, что она одинакова для разных деталей. (Нужны некоторые изменения в обозначениях, поскольку k 2 нам теперь понадобится для обозначения стоимости контроля детали № 2.) Следует ли проверять все детали или только некоторые? Если только отдельные, то какие? Используем аппроксимацию равенства (3).

Различие между двумя планами будет в пользу плана 2 на величину

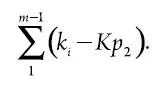
Какую деталь проверять, а какую не проверять, чтобы минимизировать полные затраты? Другими словами, как можно максимизировать разницу между двумя планами? Ответ очевиден. Расположим M членов ряда