Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

Идея состояла в том, что сильное взаимодействие не может изменить странность частицы, так что если две частицы имеют разную странность, то распад одной в другую через сильное взаимодействие невозможен. На пути в нижнюю ложбину стоит барьер. Однако слабое взаимодействие может изменить странность. Поэтому, раз дельта-барион распадается в протон через сильное взаимодействие, обе эти частицы имеют одинаковую странность, равную 0; в то же время сигма-гиперон имеет другое значение странности, так как для его распада в протон необходимо слабое взаимодействие, и ему приписали странность, равную –1. То, что это значение получилось отрицательным, связано только с причудами нумерации разных частиц. Если бы оно было равно 1, а не –1, ничего не изменилось бы.

Затем были обнаружены еще более экзотические частицы, возникающие в высокоэнергетических столкновениях, – они распадались в два этапа. Их назвали каскадными частицами и предположили, что они обладают двойной странностью, то есть имеют странность, равную –2. Результат первого этапа распада имеет странность –1 и распадается на протоны и нейтроны, имеющие нулевую странность. Это несколько похоже на фокус с вытягиванием кролика из шляпы, но он составляет часть научного процесса. В науке то и дело приходится извлекать что-нибудь из шляпы. Большую часть извлеченного приходится отбрасывать, так как она ни на что не годится. Но, если вытаскивать достаточно долго, рано или поздно попадется кролик. Гелл-Манн рассказывал: «Я придумал теорию странности, когда объяснял кому-то одну неправильную идею: я случайно оговорился, и получилась теория странности». Как оказалось, странность была в высшей степени замечательным кроликом.

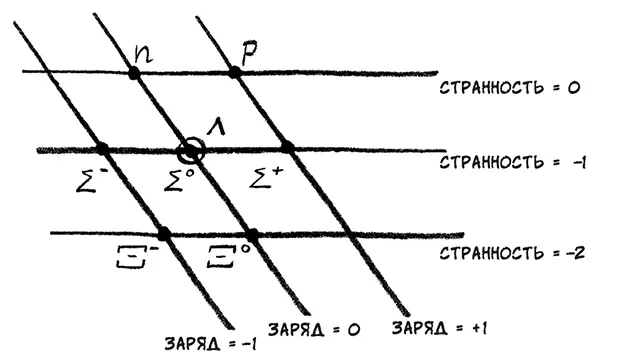
Исходно понятие странности было введено в качестве бухгалтерского фокуса, приема, который облегчал учет каналов распада из одних частиц в другие. Никто не предполагал, что в идее странности содержится какой бы то ни было физический смысл. Она была нужна, только чтобы установить очередной набор клеток в зоопарке частиц. Но эта новая характеристика оказалась первым намеком на существование гораздо более глубокой физической реальности, действующей под всеми этими частицами. Ключевой момент настал, когда частицы со сходной массой нанесли на график, связывающий значения странности и электрического заряда. Получившаяся картина была преисполнена симметрии.

Частицы расположились по шестиугольной решетке, причем в центральной точке этой решетки находились сразу две частицы. Если пионы и каоны расположить на графике зависимости странности от заряда, то тоже получается сходная структура. Когда получаешь такую конструкцию, это несомненно что-то значит. Ключ к пониманию более глубокой реальности, лежащей за этими частицами, состоял в осознании того, что шестиугольные структуры, которые они образовывали, не были чем-то новым – они встречались и раньше. Не в физике, а в математике симметрии.

Для человека, изучавшего математику симметрии, такая шестиугольная система клеток со сдвоенной точкой в центре выглядит очень знакомо. Она является визитной карточкой вполне конкретного симметричного объекта, называемого группой SU(3).

На мой взгляд, это великолепно. Про симметрию я знаю. У меня появляется шанс понять, что происходит в глубинах моей игральной кости. Собственно говоря, моя кость – это идеальное средство объяснения идей, которые лежат в основе математики симметрии. Преобразованиями симметрии такого кубика (если пренебречь очками на его гранях) называются все способы взять кубик, повернуть его и положить обратно так, чтобы он выглядел точно таким же образом, как раньше. Всего таких движений существует 24. Например, кубик можно просто повернуть на четверть оборота вокруг одной из граней или повернуть его на треть оборота вокруг одной из осей, проходящих через противоположные углы кубика.

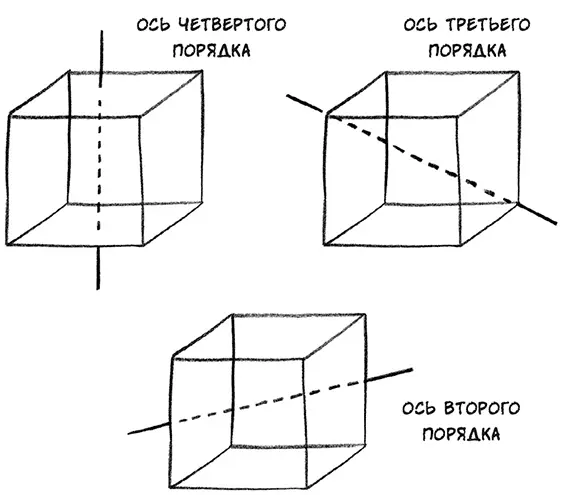
Всего разных вариантов действий существует 24 (включая тот странный вариант, в котором кубик вообще можно оставить в покое и ничего с ним не делать). Этот набор симметричных движений называют S 4 или группой симметрии четвертого порядка. С учетом зеркальной симметрии, то есть того обстоятельства, что кость также можно увидеть в зеркальном отражении, у такого кубика имеется 48 разных симметрий.

Кубик следует рассматривать как геометрическую форму в трехмерном пространстве, на которую воздействует группа симметрии S 4. Но существуют и другие геометрические формы, имеющие те же симметрии. Например, другой трехмерной геометрической формой, группа симметрии которой та же, что и у куба, является октаэдр. Кроме того, существуют объекты более высоких размерностей, также имеющие группу симметрии S 4. Таким образом, имеется много разных геометрических форм, в основе которых лежит одна и та же группа симметрии.

В основе шестиугольной схемы систематизации частиц лежит не группа симметрии игральной кости, а другой симметричный объект, называемый SU(3). Обозначение SU(3) означает «специальная унитарная группа третьего порядка», но такая группа может описывать симметрии разных геометрических объектов разной размерности. Шестиугольная решетка, образованная частицами, совпадает с конструкцией, которую математики используют для описания воздействия SU(3) на объект в восьмимерном пространстве. Восемь частиц, образующих решетку, соответствуют числу измерений, необходимых для создания такого симметричного объекта.

Этот шестиугольник стал тем розеттским камнем, который открыл для физики элементарных частиц совершенно новое направление, хотя для описания этого переворота обычно используют другую культурную аналогию. Путеводный свет этой фигуры с восемью частицами, соответствующей такому восьмимерному представлению, привел к так называемому «восьмеричному пути», название которого цитирует буддистскую идею восьмеричного пути к духовному просветлению.

Существуют и другие фигуры, соответствующие объектам разных размерностей, на которые может воздействовать SU(3). Восхитительное откровение состояло в том, что эти другие схемы можно использовать для расположения других обитателей нашего зверинца частиц. Оказалось, что разные геометрические представления симметрий группы SU(3) отвечают за разные физические частицы, из которых состоит материя Вселенной.

Я не перестаю поражаться тому, как физический мир снова и снова оказывается математическим объектом. Спрашивается, в том ли тут дело, что математика просто дает удобные средства для связного описания физической Вселенной, или же физическая Вселенная на самом деле является физическим проявлением математического объекта? Эта новая связь превратила физические частицы в геометрические элементы, стабилизированные группой симметрии, действующей в геометрическом пространстве.