Макс Тегмарк - Наша математическая вселенная. В поисках фундаментальной природы реальности

Метод параллакса, который работал для ближайших звезд, не годился для туманностей: они настолько далеко, что их параллактические углы слишком малы для измерения. Как еще можно измерить большие расстояния? Если посмотреть в телескоп на далекую лампочку, можно заметить, что на ней напечатано «100 ватт», и это все, что вам нужно: просто воспользуйтесь законом обратных квадратов и вычислите, как далеко она должна находиться, чтобы иметь наблюдаемую яркость. Астрономы называют такие полезные объекты известной светимости стандартными свечами . Применяя вышеупомянутый детективный метод, астрономы с сожалением обнаружили, что звезды вовсе не стандартизированы: некоторые светят в миллион раз ярче Солнца, а другие в тысячу раз слабее. Однако если вы сможете, наблюдая звезду, увидеть, что на ней написано «4 × 10 26ватт» (корректная маркировка для нашего Солнца), у вас появится стандартная свеча и возможность вычислить расстояние до нее точно так же, как до лампочки. К счастью, природа снабдила нас особым типом полезных в этом отношении звезд – их называют цефеидами . Это переменные звезды, светимость которых колеблется во времени из-за того, что они меняются в размерах. В 1912 году гарвардский астроном Генриетта Соун Ливитт обнаружила, что темп их пульсаций может служить ваттметром: чем больше дней проходит между двумя последовательными пульсациями, тем больше излучается ватт световой энергии.

У цефеид есть также то преимущество, что, будучи достаточно яркими, они видны на огромных расстояниях (некоторые из них светят в 100 тыс. раз ярче Солнца). Американский астроном Эдвин Хаббл открыл несколько таких звезд в Туманности Андромеды – диффузном пятнышке размером с Луну, которое можно увидеть невооруженным глазом, если забраться подальше от городских огней. Используя калифорнийский телескоп Хукера (его 2,5-метровое зеркало было тогда крупнейшим в мире), он измерил периоды их пульсации, рассчитал с помощью формулы Ливитт, какой они обладают светимостью, сравнил с их видимым блеском и вычислил расстояния до них. Когда он рассказал о своих результатах на конференции в 1925 году, у многих отвисли челюсти: он доказал, что Туманность Андромеды – это галактика примерно в 1 млн световых лет от нас, в тысячу раз дальше самых далеких звезд, которые моя бабушка видела на ночном небе! Теперь мы знаем, что Туманность Андромеды находится еще дальше – примерно в 3 млн световых лет, так что Хаббл невольно продолжил традицию ошибочной недооценки расстояний, идущую от Аристарха Самосского и Коперника.

Хаббл и другие астрономы продолжали открывать все более далекие галактики. Они раздвинули наши горизонты с миллионов до миллиардов световых лет, а мы в гл. 5 раздвинем их до триллионов световых лет и даже дальше.

Так тянется ли космос бесконечно? К вопросу можно подойти двояко: путем наблюдений и теоретически. Пока мы следовали первому подходу, рассматривая, как хитроумные измерения открывали все более далекие области космоса без видимых признаков конца. Однако и теоретики достигли значительного прогресса. Прежде всего, как может пространство не тянуться бесконечно? Я объяснил детям, что было бы странно вдруг встретить знак, как на рис. 2.6, предупреждающий о достижении конца космоса. Я размышлял об этом, когда сам был ребенком: а что за этим знаком? Мне казалось, что беспокоиться о достижении конца космоса столь же глупо, как древним мореплавателям бояться упасть с края Земли. Так что я попросту заключил, что пространство бесконечно и тянется вечно. Еще Евклид пришел к выводу, что геометрия является частью математики и что бесконечное трехмерное пространство можно описать столь же строго, как и другие математические структуры вроде числовых множеств. Древнегреческий ученый разработал красивую математическую теорию бесконечного трехмерного пространства, а также его геометрических свойств, и люди долго считали ее единственным логически возможным способом существования нашего физического пространства.

Рис. 2.6.Трудно представить себе, что пространство может быть конечным. Если оно где-то заканчивается, то что находится дальше, за его краем?

Однако в середине XIX века математики Карл Фридрих Гаусс, Янош Бойяи и Николай Лобачевский независимо друг от друга открыли, что существуют и другие логические возможности для однородного трехмерного пространства. Бойяи в восторге писал отцу: «Из ничего я создал странный новый мир». Новые пространства подчиняются новым правилам: так, они более не обязаны быть бесконечными, каковым представлялось пространство Евклиду, а углы треугольника не обязательно дают в сумме 180°. Представьте себе треугольники на двумерных поверхностях трехмерных фигур. Сумма трех их углов больше 180° на сфере ( рис. 2.7 , слева), 180° на цилиндре (в середине) и меньше 180° на гиперболоиде (справа). Более того, двумерная поверхность сферы конечна, хотя на ней нет ничего похожего на край.

Этот пример показывает, что правила евклидовой геометрии могут нарушаться на поверхности, если она не плоская. Однако идеи Гаусса и других математиков были еще радикальнее: пространство может быть искривленным само по себе, даже если оно не является поверхностью чего-либо! Предположим, вы – слепой муравей, желающий знать, по какой из фигур на рис. 2.7 вы ползаете. Вы чувствуете себя так, будто живете в двумерном пространстве, поскольку не можете выйти в третье измерение (оторваться от поверхности), но это не препятствует вашей детективной работе: вы по-прежнему можете определить прямую линию (как кратчайший путь между двумя точками), а значит, и суммировать величины трех углов треугольника. Например, если вы получите 270°, то воскликнете: «Это больше 180°, значит, я на сфере!» Чтобы еще больше впечатлить друзей-муравьев, вы даже можете рассчитать, как далеко нужно пройти по прямой, чтобы вернуться в исходную точку. Иными словами, все обычные для геометрии объекты – точки, прямые, углы, кривые и т. д. – можно строго определить, оставаясь в двумерном пространстве безо всяких ссылок на третье измерение. Это означает, что математики могут строго определить кривизну двумерной поверхности, даже если третьего измерения не существует: двумерное пространство может быть искривленным само по себе, не являясь поверхностью чего-либо.

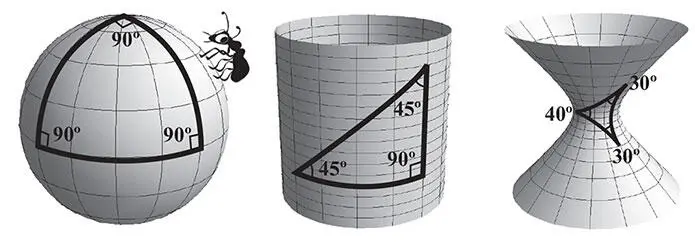
Рис. 2.7.Если нарисовать треугольники на этих поверхностях, сумма их углов окажется больше 180° ( слева ), 180° ( посередине ) и меньше 180° ( справа ). Эйнштейн считал, что в нашем трехмерном физическом пространстве для треугольников возможны все эти варианты.