Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

Если начать с частицы, находящейся внутри связной области размером Δx , то, как мы установили, с течением времени она может оказаться где угодно внутри более крупной области размером x .

Эта ситуация показана на рис. 4.5. Точнее говоря, это значит, что, если бы мы искали частицу в начальный момент, были бы шансы найти ее где-то во внутренней области. Если бы мы не стали проводить измерения, а решили подождать, высоки были бы шансы найти ее где-то во внешней, более крупной связной области. Это значит, что частица могла перейти из точки внутри малой начальной области в точку внутри более крупной. Однако она не обязана была двигаться, так что до сих пор есть вероятность нахождения ее в меньшей области Δx . Но вполне возможно, что измерения покажут, что частица дошла как раз до края большой области [14] Есть вероятность, что частица продвинется еще дальше, чем в «предельном» случае, ограниченном большой окружностью на рисунке, но, как мы уже показали, сложение циферблатов приводит к отмене таких сценариев. . Если бы этот предельный случай был реализован при измерении, то мы заключили бы, что частица движется с импульсом, который задается только что выведенным нами уравнением (если вы не следовали за нашими математическими рассуждениями, просто примите это на веру), то есть p = h / Δx .

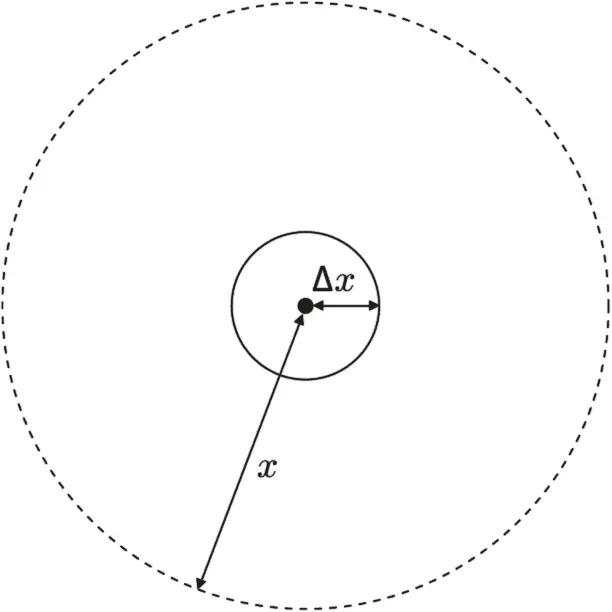
Рис. 4.5. Небольшая область со временем растет, в то время как изначально локализованная там частица с течением времени делокализуется

Теперь можем опять начать сначала и вернуть все в исходное положение. Частица опять окажется в малой области размера Δx . После измерения мы, вероятно, найдем частицу в какой-то другой точке внутри более крупной области, до границы, и таким образом придем к выводу, что ее импульс меньше предельного значения.

Если мы представим, что вновь и вновь повторяем этот эксперимент, измеряя импульс частицы, которая первоначально находится внутри небольшой области размером Δx , мы обычно будем получать при измерении множество значений p где-то между нулем и предельным значением h / Δx . Фраза «если проделать этот эксперимент несколько раз, то можно предсказать, что измеренный импульс окажется в пределах между нулем и h / Δx » значит, что «импульс частицы имеет неопределенность h / Δx ». Как и в случае с неопределенностью положения, физики ввели для неопределенности этого рода символ Δp и пишут, что ΔpΔx ~ h. Значок ~ обозначает, что произведение неопределенностей положения и импульса примерно равно постоянной Планка – оно может быть или немного больше, или немного меньше. Немного углубившись в математику, можно сделать это уравнение еще более точным. Результат будет зависеть от подробностей расположения первоначальной группы циферблатов, но не стоит тратить на него слишком много сил и времени, потому что уже сделанного достаточно, чтобы понять основные идеи.

Утверждение, что неопределенность положения частицы, умноженная на неопределенность ее импульса (приблизительно), равна постоянной Планка – возможно, самая известная формулировка принципа неопределенности Гейзенберга. Эта формулировка гласит: если мы знаем, что частица находится в какой-то исходный момент времени в какой-то области, то измерение положения частицы в какой-то более поздний момент времени покажет, что частица движется с импульсом, значение которого нельзя предсказать точнее, чем «нечто между нулем и h / Δx ». Иными словами, если мы будем все больше и больше сужать начальную область нахождения частицы, она будет стремиться отпрыгнуть от этой области все дальше. Это настолько важно, что заслуживает третьего варианта формулировки: чем точнее вы знаете положение частицы в какой-то момент, тем хуже будете знать скорость ее движения и, соответственно, ту точку, в которой она окажется позже.

Эта формулировка принципа неопределенности как раз и принадлежит Гейзенбергу. Она лежит в основе квантовой теории, но тут мы должны четко заявить, что сам по себе принцип вовсе не является неопределенным. Это утверждение о нашей неспособности точного отслеживания частицы, и здесь не больше места для квантового волшебства, чем в ньютоновой физике. На последних нескольких страницах мы вывели принцип неопределенности Гейзенберга из фундаментальных правил квантовой физики, которые соответствуют правилам хода часов, сложения и вычитания циферблатов. И действительно, его происхождение кроется в нашем допущении, что частица через мгновение после измерения ее положения может оказаться в любом другом месте Вселенной. Диковатость нашего первого предположения, что частица может оказаться в совершенно произвольном месте Вселенной, была приручена с помощью неконтролируемой квантовой интерференции, и принцип неопределенности – это в каком-то смысле все, что осталось от исходной анархии.

Прежде чем двинуться дальше, мы должны сказать еще нечто очень важное об интерпретации принципа неопределенности. Не следует впадать в заблуждение, думая, что частица находится в каком-то конкретном единственном месте и что распространение исходных циферблатов отражает лишь ограниченность нашего понимания. Если мы считаем, что не можем правильно вывести принцип неопределенности, потому что не можем признать необходимость рассматривать все циферблаты из всех точек внутри исходной области, можно перемещать их по очереди в отдаленную точку Х и потом складывать. Именно делая это, мы и получили наш результат, то есть нам пришлось предположить, что частица прибывает в Х через суперпозицию многих возможных маршрутов.

Принципом Гейзенберга мы чуть позже воспользуемся для иллюстрации некоторых примеров из реального мира. Сейчас же достаточно и того, что нам удалось вывести один из ключевых результатов квантовой теории, не пользуясь ничем другим, кроме простых манипуляций с воображаемыми циферблатами.

Подставим в уравнения несколько цифр, чтобы добиться лучшего понимания предмета. Сколько нужно ждать возникновения существенной вероятности, что песчинка выпрыгнет из спичечного коробка? Предположим, что спичечный коробок имеет стенки длиной 3 см, а песчинка весит 1 мкг. Напомним, что условие для появления существенной вероятности перемещения песчинки на заданное расстояние определяется неравенством

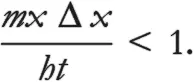
где Δx – размер коробка. Теперь подсчитаем, каким должно быть время t , если мы хотим, чтобы песчинка покрыла расстояние x = 4 см, что уверенно превосходит размеры спичечного коробка. С помощью очень несложной алгебры находим, что