Нейт Сильвер - Сигнал и шум. Почему одни прогнозы сбываются, а другие – нет

Однако мы не можем наблюдать эту зависимость напрямую. Вместо этого мы имеем набор отдельных точек, характеризующих данные, на базе которых мы должны найти закономерность. Кроме этого, на эти точки данных влияет масса своеобразных обстоятельств – иными словами, у нас имеются и сигнал, и некоторый шум.

На график я нанес 100 точек данных, представленных в виде кругов и треугольников. Этого должно быть достаточно для выявления сигнала даже с учетом шума. Хотя в данных и присутствует некая доля случайности, вполне понятно, что они в целом следуют нашей кривой.

Но что произойдет, если объем данных, имеющийся в нашем распоряжении, окажется более ограниченным (как обычно и происходит в реальной жизни)? Очевидно, что это приведет к увеличению ошибки. На графике, приведенном на рис. 5.5a, показаны примерно 25 точек из сотни. Каким образом вы могли бы теперь соединить эти точки?

Рис. 5.5а.Ограниченная выборка данных

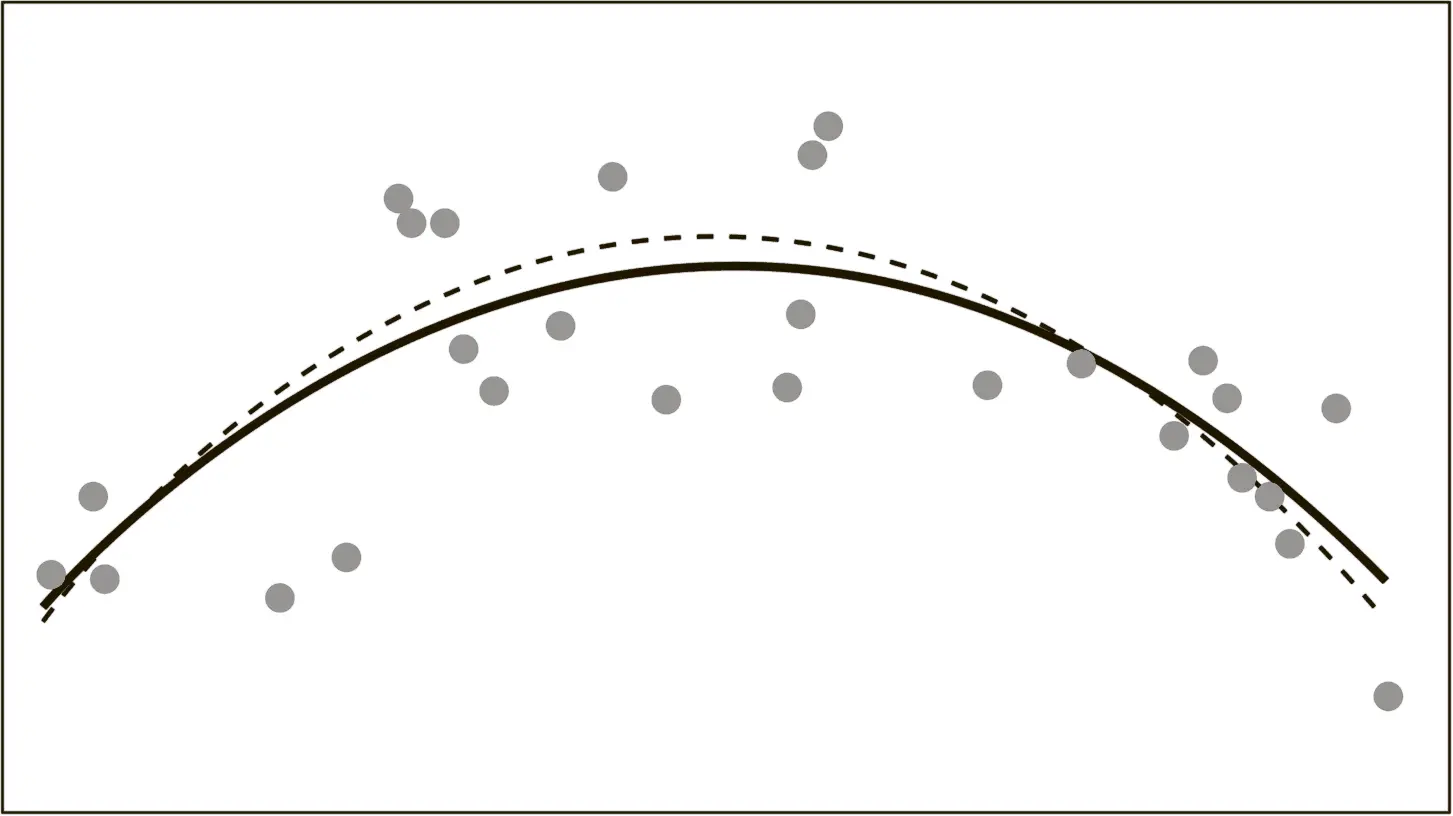
Рис. 5.5б.Хорошо подобранная модель

Разумеется, зная, как должна выглядеть подлинная тенденция, вы будете склонны соединять точки в виде некоторой кривой. На практике моделирование таких данных с помощью простого математического инструмента, известного как квадратное уравнение, действительно помогает выявить связь, очень похожую на истинную (рис. 5.5б).

В ситуациях, когда мы не знаем, какими должны быть наши данные, но хотим, чтобы они соответствовали «платоническому идеалу», мы часто склонны проявлять жадность. На рис. 5.5в отражен результат такого поведения – модель с оверфиттингом. При создании этого графика была разработана комплексная функция {354}, которая отыскивает каждую из отдаленных точек данных. При попытке «увязать» их между собой значение функции колеблется (довольно невероятным образом) вверх и вниз. И в результате мы еще больше удаляемся от понимания истинной связи, и прогнозы, которые мы делаем, становятся еще менее качественными.

Казалось бы, что избежать подобной ошибки легко, но только в том случае, если бы мы были всемогущи и всегда представляли себе структуру данных. Однако почти всегда в реальных условиях нам приходится действовать по индукции [79], находя структуру на основе имеющихся данных. Скорее всего, в вашей модели будет проявляться оверфиттинг, когда объем данных ограничен, сами данные засорены шумом, а ваше понимание фундаментальных связей достаточно слабо. И эти обстоятельства принимаются во внимание при прогнозировании землетрясений.

Когда мы не знаем об истинной связи или не хотим об этом знать, у нас появляется множество причин, по которым мы будем склоняться к оверфиттингу. Одна из них состоит в том, что модель с оверфиттингом будет лучше соответствовать результатам большинства статистических тестов, используемых прогнозистами. Например, довольно часто встречается тест, который оценивает разброс данных в модели. Судя по его результатам, модель с оверфиттингом (см. рис. 5.5в) позволяет объяснить 85 % дисперсии. И благодаря этому она выглядит «лучше», чем модель с хорошей степенью подгонки (см. рис. 5.5б), объясняющая лишь 56 %. Однако, по сути, модель с оверфиттингом обеспечивает такие высокие результаты за счет своеобразного обмана – она скорее принимает во внимание шум, а не сигнал. То есть на самом деле она обладает меньшей степенью достоверности при объяснении событий в реальном мире {355}.

Рис. 5.5 в.Модель с оверфиттингом

Несмотря на всю очевидность приведенного выше объяснения, многие прогнозисты полностью игнорируют эту проблему. Значительное количество статистических методов, имеющихся в распоряжении исследователей, позволяет им вести себя подобно ребенку, пытающемуся увидеть в формах облаков изображения зверей (это занятие, безусловно, очень интересное, но совершенно ненаучное) [80]. Математик Джон фон Нейман говорил об этой проблеме так: «Кривую с четырьмя параметрами я могу подогнать под слона, а с пятью – я заставлю слона махать хоботом» {356}.

Оверфиттинг представляет собой двойную проблему: он помогает нашей модели лучше выглядеть на бумаге, однако в действительности показывать худшие результаты. И из-за второй проблемы модель с оверфиттингом, применяемая для создания реальных прогнозов, в какой-то момент сильно нас подведет. А первая проблема будет создавать для нашей модели слишком впечатляющий образ (опять же до поры). Она будет считаться очень точной и заслуживающей доверия, подлинным шагом вперед по сравнению с прежними техниками. Это даст возможность опубликовать ее в научных изданиях, вытеснив с рынка другие модели, показывающие более честную картину. Но если модель включает в себя шум, у нее есть немалый потенциал для того, чтобы повредить научным результатам.

Как вы, возможно, уже догадались, модель прогнозирования землетрясений Кейлиса-Борока обладала огромным оверфиттингом. В ней использовался невероятно сложный набор уравнений, примененных к данным с большой долей шумов. За это пришлось заплатить свою цену – из 23 прогнозов, сделанных на ее основе, лишь три оказались верными. Дэвид Боумэн признал, что в созданной им модели имелись аналогичные проблемы, и вовремя перестал над ней работать.

Должен сразу сказать, что эти ошибки, как правило, представляют собой вполне искренние заблуждения. Если воспользоваться названием другой книги, то они отражают нашу склонность быть одураченными случайностью [81]. Особенности нашей модели могут казаться нам вполне объяснимыми и допустимыми. Мы даже можем, в полной мере этого не осознавая, работать в обратном направлении и создавать убедительно звучащие теории, позволяющие рационализировать нашу точку зрения и тем самым дурачить и самих себя, и своих друзей с коллегами. Майкл Бабяк, много писавший об этой проблеме {357}, характеризует дилемму следующим образом: «В научной работе мы стараемся выстроить баланс между любопытством и скепсисом».

И любопытство часто берет над нами верх.

Наша склонность ошибочно принимать шум за сигнал способна время от времени приводить к вполне печальным последствиям в реальной жизни. Япония, несмотря на высокую степень сейсмической активности в регионе, оказалась практически неготовой к разрушительному землетрясению 2011 г. Ядерный реактор в Фукусиме был способен выдержать землетрясения магнитудой до 8,6 балла {358}, но никак не 9,1 балла. Археологические находки позволяют предположить, что в прежние времена высота цунами могла достигать 40 м {359}(что и произошло после землетрясения 2011 г.), однако эти случаи были, по всей видимости, забыты или проигнорированы.