Стивен Строгац - Удовольствие от X. Увлекательное путешествие в мир математики от одного из лучших преподавателей в мире

Сегодня ситуация не изменилась. «Папа, ты можешь показать мне, как делать эти примеры на умножение?» «Конечно могу», – самонадеянно заявил я, пока не довел дочь до истерики. «Нет, папа, сейчас это делают не так! Это устаревший способ! Разве ты не знаешь умножения методом решетки? Нет? Ну а как насчет частичных произведений?»

Эта унизительная ситуация побудила меня пересмотреть процесс умножения с самого начала {9} 9 Кит Девлин написал провокационную серию очерков о природе умножения: что это такое, что в нем не так и почему определенные виды мышления более ценны и надежны в процессе умножения, чем другие. Он рассматривает умножение как масштабирование, не сводя его к процессу суммирования, и показывает, что эти два понятия (умножение как масштабирование и умножение как суммирование) существенно разнятся в реальных условиях. См. его январскую (2011 года) статью What exactly is multiplication? на http://archive.is/qCkK , а также три более ранних 2008 года: It ain’t no repeated addition ( http://www.maa.org/devlin/devlin_06_08.html ), It’s still not repeated addition ( http://www.maa.org/devlin/devlin_0708_08.html ) и Multiplication and those pesky British spellings ( http://www.maa.org/devlin/devlin_09_08.html ). Эти статьи активно обсуждались в среде блогеров, особенно среди учителей. . И оно, как только вы вникнете в него глубже, действительно оказывается очень тонкой вещью.

Возьмите, например, терминологию. Равно ли трижды семь сумме трех по семь? Или сумме семи по три?

В некоторых культурах язык менее неоднозначен. Один мой друг из Белиза привык читать таблицу умножения так: «Семь один раз – это семь, семь дважды – четырнадцать, семь трижды – двадцать один» и так далее. Такая формулировка позволяет понять, что первое число это множимое, а второе – множитель. Аналогичная игра слов есть и в бессмертных стихах песни Лайонела Ричи [3] Американский исполнитель поп-музыки, снискавший мировую славу в 1980-х годах. Прим. ред. «Она однажды, дважды, трижды леди». (Слова «Она леди три раза» никогда не стали бы хитом.)

Может быть, вся эта суета вокруг семантики кажется вам глупой, так как порядок, в котором числа перемножаются, не имеет никакого значения, то есть в любом случае 7 × 3 = 3 × 7. Хорошо, но тут напрашивается вопрос, на котором я хотел бы остановиться подробнее. Является ли этот переместительный (коммутативный) закон умножения a × b = b × a действительно таким очевидным? Помню, меня еще в детстве он удивил, возможно, и вас тоже.

Чтобы привнести немного магии, представьте себе, что вы не знаете, чему равно 7 × 3, и поэтому складываете семерки: 7, 14, 21. Теперь поменяйте местами сомножители и складывайте тройки, получается 3, 6, 9… Чувствуете ли вы все нарастающее недоумение? До сих пор ни одно из чисел в этих перечнях не совпало, но пройдем дальше… 12, 15, 18, и затем – ах! – 21.

Я хочу сказать, что если вы считаете, что умножение соответствует многократному суммированию определенного числа (другими словами, многократному сложению), то коммутативный закон не совсем понятен. Но все проясняется, если представить умножение визуально. Допустим, 7 × 3 – это число точек в прямоугольной матрице с семью строками и тремя столбцами.

Если поставить матрицу набок, она превращается в матрицу, состоящую из трех строк и семи столбцов. Поскольку сама картинка при вращении не изменяется (то есть количество точек сохраняется), то похоже на то, что действительно 7 × 3 = 3 × 7.

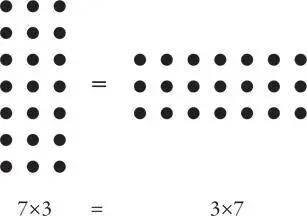
Тем не менее, как ни странно, во многих реальных ситуациях, особенно когда дело касается денег, люди, кажется, забывают о коммутативном законе умножения. Позвольте привести два примера.

Предположим, вы собрались купить новые джинсы. Их продают со скидкой 20% от цены 50 долларов, указанной на этикетке, что выглядит заманчиво, но имейте в виду, что вам также придется заплатить 8% налога с продаж. После того как продавщица закончит нахваливать, как великолепно джинсы на вас сидят, и начнет оформлять покупку, она сделает паузу и заговорщицки шепнет: «Позвольте мне сэкономить ваши деньги. Я сначала посчитаю налог, а затем 20%-ную скидку от полученной суммы. Хорошо?»

Но что-то вас смущает. «Нет, спасибо, – говорите вы. – Не могли бы вы сначала вычесть 20%-ную скидку, а затем снять налог с цены покупки? Тогда я заплачу меньше».

Какой способ более выгоден для вас? (Предположим, что оба законны.)

Столкнувшись с подобной задачей, многие решают ее последовательным суммированием . Они вычисляют налоги и скидки в соответствии с заданным сценарием, а затем, чтобы определить окончательную цену, выполняют необходимое сложение или вычитание.

Если вы согласитесь с продавцом, то налог составит 4 доллара (8% от цены на этикетке). И цена джинсов увеличится до 54 долларов. Тогда при 20%-ной скидке от 54 долларов возвращенная сумма будет равняться 10,80 доллара. Итак, в конечном счете вы заплатите 54 доллара минус 10,80 доллара, что в сумме даст 43,20 доллара.

В соответствии же с вашим сценарием сначала будет вычитаться 20% скидки (на чем вы сэкономите 10 долларов от цены на этикетке). Тогда 8% налога на льготную цену в 40 долларов составят 3,20 доллара, так что вы все равно в конечном итоге заплатите 43,20 доллара. Удивительно?!

Но это же просто коммутативный закон в действии. Чтобы это понять, необходимо думать в стиле последовательного умножения , а не последовательного сложения. 8% налога и последующая за ним 20%-ная скидка вычисляются путем умножения цены на этикетке на 1,08 и последовательным умножением полученного результата на 0,80. Изменение порядка вычисления налога или скидки просто меняет местами сомножители, но, поскольку выполняется равенство 1,08 × 0,80 = 0,80 × 1,08, окончательная цена получается одинаковой {10} 10 В примере с джинсами порядок применения налогового сбора и скидки для вас не имеет значения – в обоих сценариях вы в конечном итоге платите 43,20 доллара. Но для правительства и магазина он весьма существенен! В сценарии продавщицы (при котором вы платите налог в зависимости от первоначальной цены) вы заплатите 4 доллара налога, в вашем сценарии – всего 3,20 доллара. Я не знаю, одинаков ли закон о налоге на продажи во всех штатах, но рациональнее всего взимать его на основе фактической цены в магазине. Дальнейшее обсуждение этих вопросов см. http://www.facebook.com/TeachersofMathematics/posts/166897663338316 . .

Соображения, подобные этим, возникают и при принятии решений о больших финансовых сделках. Лучше или хуже традиционного пенсионного плана новый план недавно, принятый Конгрессом США (закон Roth 401(k)) {11} 11 Обсуждение достоинств и недостатков закона Roth 401(k) см. публикации Commutative law of multiplication ( http://thefinancebuff.com/commutative-law-of-multiplication.html ) и The new Roth 401(k) versus the traditional 401(k): Which is the better route? ( http://www.thesimpledollar.com/2007/06/20/the-new-roth-401k-versus-the-traditional-401k-which-is-the-better-route/ ). ? И вообще, если у вас есть куча денег, которые вы намерены инвестировать, но на них нужно платить налоги, то когда лучше это делать – в начале инвестиционного периода или в конце?