Рудольф Баландин - 100 великих загадок географии

Температура мантии около двух тысяч градусов. Плотность её увеличивается с глубиной четырьмя ступенями, позволяющими выделить четыре слоя. Мантия – обширнейшая область высоких давлений и температур.

С глубины 2900 км плотность пород быстро меняется от 11,54 до 14,2. Отсюда начинается ядро Земли, в котором выделяют ещё центральное ядрышко плотностью более 17 (в 17 раз плотней воды). У него есть свойство жидкости: в нём угасают продольные волны, которые возникают при сжатии и расширении, как это бывает с пружиной. (Поперечные волны подобны волнам на море.)

Из чего состоит земное ядро – остаётся загадкой. Оно сдавлено со всех сторон чудовищными силами гравитации. Поэтому плотнейшая внутренняя часть планеты становится текучей, как жидкость.

Из-за равных и направленных к центру гравитационных сил все внутренние сферы стремятся к равновесию, покою. В них вряд ли идут активные химические реакции.

В последние десятилетия популярна гипотеза о круговоротах вещества в мантии. Это весьма сомнительно. Там вещество необычайно плотное и находится под равномерным давлением со всех сторон. Его перемещения не могут быть значительными, а тем более сопоставимыми по скорости с движениями литосферы.

Оболочки Земли распределены по плотности. Наименее плотная и наиболее подвижная – атмосфера. Более плотная и менее подвижная – гидросфера. Ещё инертней и плотней – литосфера. Следует ожидать, что значительно более плотная, чем она, мантия планеты должна быть существенно инертней земной коры.

Гравитационные силы сдавливают Землю равномерно со всех сторон. Казалось бы, земная кора должна иметь одинаковую толщину, а поверхность планеты – быть ровной, если не считать воронок и кратеров от ударов астероидов, как на Луне. Почему же рельеф земной коры не только сложный и разнообразный – от глубочайших впадин до высочайших вершин – и подчинён некоторым закономерностям?

Этот вопрос позже мы обдумать особо. Он связан не только с наукой геоморфологией, которая изучает происхождение рельефа, а затрагивает весь комплекс наук о Земле – и географических, и геологических.

…По-новому раскрывается в геологии время, которое не имеет смысла без материальных проявлений. «Геологическими часами» могут служить скорость накопления осадков, смены форм ископаемых животных и растений, радиоактивные минералы.

Теория относительности предполагает изменение свойств объектов при скоростях, приближающихся к скорости света (увеличение массы, «сплющивание»). Это – виртуальные явления, отражающие точку зрения наблюдателя при некоторых условных допущениях. Совсем иначе – в реальной земной природе.

При геологических медленных скоростях – в масштабах тысяч и миллионов лет – по-настоящему меняются свойства природных объектов. Скальные породы обретают пластичность и сминаются в складки, как пластилиновые. Моря блуждают по поверхности континентов. Реки, змеящиеся по равнине, переползают с места на место. Берега океанов как бы тают от постоянной волновой эрозии. Острова выныривают там, где теперь море. Континенты и островные дуги перемещаются…

Мы привычно считаем геометрию разделом абстрактной науки математики. Хотя этот термин в переводе с греческого означает «землемерие». Таким было начальное предназначение геометрии. Из практической области знаний она перешла в теоретическую.

2200 лет назад греческий математик Евклид создал логичную чёткую систему геометрии, которую назвали евклидовой. Она считалась единственно возможной, а её законы – применимыми везде и всегда.

Есть, скажем, теорема: сумма углов треугольника равна двум прямым, 180°. Она доказывается убедительно. Можно для проверки на практике подсчитать, чему равна сумма углов треугольников. И тут выяснится, что многое зависит от того, каковы размеры данных фигур.

Если вычертить на ровной поверхности Земли треугольник длиной в сотни километров и точно измерить его углы, то сумма их окажется меньше 180°. Это понятно: углы треугольника искажены, потому что вычертили его не на плоскости, а на поверхности шара. Надо чертить фигуры на плоской поверхности.

Но почему надо принимать за основу плоскую поверхность? В природе таких поверхностей мало. Любая прямая линия или плоскость являются частными случаями кривой линии или плоскости.

Эту мысль положил в основу своей геометрии Н.И. Лобачевский. Он воспользовался «подсказкой», которую дала ему шарообразная форма Земли. Так геометрия после долгого перерыва вновь обрела непосредственную связь с природой.

Во времена Лобачевского учёные считали, что космическое пространство евклидово, а путь луча света – идеальной прямой. Однако Лобачевский предложил эту гипотезу «проверить, подобно другим физическим законам», и провести соответствующие «Астрономические наблюдения» (так писал он – с заглавной буквы).

В ту пору почти никто не принял его предложение всерьёз. А в XX веке выяснилось, что Лобачевский был прав. Недаром он утверждал, что в основании математики должны лежать понятия, «приобретаемые из природы». Оказывается, луч света может отклоняться от прямой линии, например, когда пролетает мимо массивных небесных тел.

История с геометрией Лобачевского показывает, что география помогает познавать мир и совершать открытия в разных областях знаний. И другой вывод: надо уметь переходить от абстрактных понятий математики к реальной природе. Показательный пример – гипсометрическая кривая (от греческих слов «гипсос» – «высота» и «метрос» – «измерение»). Она изображает обобщённый рельеф Земли.

Гипсометрическая кривая ведёт нас от высоких гор до океанских глубин. На ней видны две отчётливые ступени: океаническая и материковая равнины. Абстрактная гипсометрическая кривая показывает фундаментальную особенность земного рельефа.

На карте земной поверхности площадь Мирового океана значительно больше площади суши. Гипсометрическая кривая показывает то, что с поверхности не увидишь: если к территории континентов добавить площадь шельфа и материкового склона (что вполне логично), то в сумме они будут немногим меньше площади дна океана. Что бы это значило?

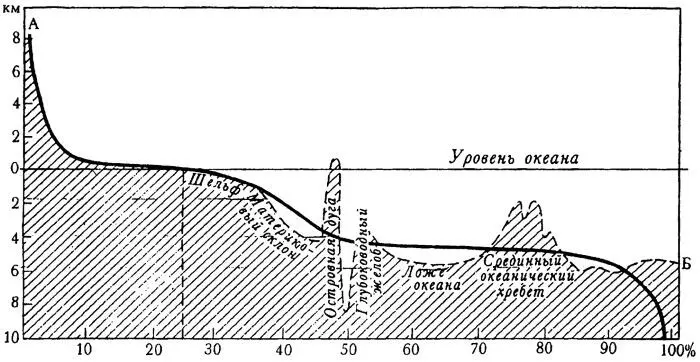
Гипсометрическая кривая (сплошная линия) и рельеф дна Мирового океана

Гипсометрическая кривая превращается в вопросительный знак, если несколько иначе нарисовать профиль дна Мирового океана, приблизив его к реальности. Взглянем на окраины Тихого океана. Там перед горными хребтами Анд и Кордильер островными дугами зияют впадины глубоководных желобов.