Яков Перельман - Головоломки. Задачи. Фокусы. Развлечения

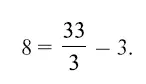
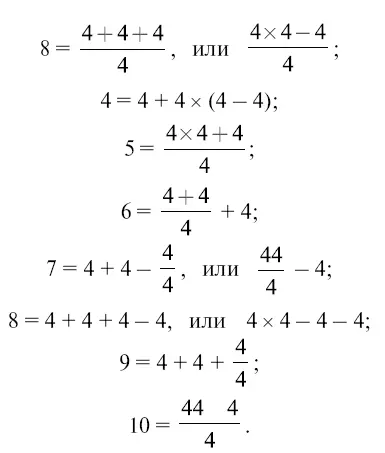
Будет только один такой год в XX веке: 1961-й.

Единственные цифры, которые не искажаются в зеркале, — это 1, 0 и 8. Значит, искомый год может содержать в себе только такие цифры. Кроме того, мы знаем, что это один из годов XIX века, т. е. что первые его две цифры 18.

Легко сообразить теперь, какой это год: 1818-й. В зеркале 1818 год превратится в 8181-й: это ровно в 4 1/ 2раза больше, чем 1818:

1818 × 4 1/ 2= 8181.

Других решений задача не имеет.

Ответ прост: 1 и 7. Других таких чисел нет.

Таких чисел сколько угодно:

3 × 1 = 3,

3 + 1 = 4,

10 × 1 = 10,

10 + 1 = 11,

и вообще всякая пара целых чисел, из которых одно — единица.

Это потому, что от прибавления единицы число увеличивается, а от умножения на единицу остается без перемены.

Числа эти 2 и 2. Других целых чисел с такими свойствами нет.

1, 2 и 3 дают при перемножении и при сложении одно и то же:

1 + 2 + 3 = 6; 1 × 2 × 3 = 6.

Таких чисел очень много. Например:

2: 1 = 2;

2 × 1 = 2;

7: 1 = 7;

7 × 1 = 7;

43: 1 = 43;

43 × 1 = 43.

Вот еще четыре пары таких чисел:

11 и 110; 14 и 35; 15 и 30; 20 и 20.

В самом деле:

11 × 110 = 1210;

15 × 30 = 450;

11 + 110 = 121;

15 + 30 = 45;

14 × 35 = 490;

20 × 20 = 400;

14 + 35 = 49;

20 + 20 = 40.

Других решений задача не имеет. Довольно хлопотливо разыскивать решения вслепую. Знание начатков алгебры значительно облегчает дело и дает возможность не только отыскать все решения, но и удостовериться, что больше пяти решений задача не имеет.

Рассуждаем так. Цифра 6 получилась от сложения колонки из двух цифр, из которых нижняя может быть либо 0, либо 5. Но если нижняя 0, то верхняя 6. А может ли верхняя цифра быть 6? Пробуем: оказывается, чему бы ни равнялась вторая цифра множителя, никак не получается 6 на предпоследнем месте первого частного произведения. Значит, нижняя цифра предпоследней колонки должна быть 5; тогда над ней стоит 1.

Теперь легко восстановить часть стертых цифр:

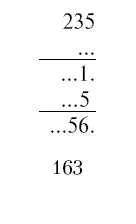
Последняя цифра множителя должна быть больше 4, иначе первое частное произведение не будет состоять из четырех цифр. Это не может быть цифра 5 (не получается 1 на предпоследнем мосте). Пробуем 6 — годится. Имеем:

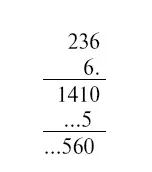
Рассуждая далее подобным же образом, находим, что множитель — 96.

Всех семеро: четыре брата и три сестры. У каждого брата три брата и три сестры; у каждой сестры четыре брата и две сестры.

Всех детей семь: шесть сыновей и одна дочь. (Обычно же отвечают, что детей двенадцать; но тогда у каждого сына было бы шесть сестер, а не одна.)

Дело объясняется очень просто. Село за стол не четверо, а только трое: дед, его сын и внук. Дед и сын — отцы, а сын и внук — сыновья.

Рассчитать, сколько лет каждому, нетрудно. Ясно, что сын старше внука в 7 раз, а дед в 12 раз. Если бы внуку был 1 год, сыну было бы 7 лет, деду — 12 лет, а всем троим вместе 20 лет. Это ровно в 5 раз меньше, чем на самом деле. Значит, в действительности внуку 5 лет, сыну 35 и деду 60.

Проверим: 5+ 35 + 60 = 100.

На удочку этой задачи легко попасться: можно думать, что если 5 землекопов в 5 часов вырыли 5 метров канавы, то для выкопки в 100 часов 100 метров понадобится 100 человек. Однако, это совершенно неправильное рассуждение: понадобятся те же 5 землекопов, не больше.

В самом деле: 5 землекопов в 5 часов выкапывают 5 метров; значит, 5 землекопов в 1 час вырыли бы 1 метр, а в 100 часов — 100 метров.

Обычно отвечают, что каждый играл по одному разу, не соображая, что трое (и вообще нечетное число) игроков никак не могут играть каждый только по одному разу: с кем же тогда играл третий игрок? В каждой партии должно ведь участвовать два партнера. Если играли А, В и С и сыграно было три партии, то это значит, что играли

А с В ,

А с С,

В с С .

Легко видеть, что каждый играл не по одному разу, а по два:

А играл с В и с С ,

В «с А и с С ,

С «с А и с В.

Итак, правильный ответ на головоломку таков: каждый из троих играл по два раза, хотя сыграно было всего три партии.

Ни тот, ни другая не старше: они близнецы, и каждому из них в данное время по 6 лет.

Возраст находят простым расчетом: через два года мальчик будет на 4 года старше, чем два года назад, и притом вдвое старше; значит, 4 года — это возраст его два года назад, и, следовательно, сейчас ему 4 + 2 = 6 лет.

Таков же и возраст девочки.

Через 10 суток и 1 день. В первые 10 суток улитка поднимется на 10 метров, по 1 метру в сутки; в течение же одного следующего дня она всползет еще на 5 метров, т. е. достигнет верхушки дерева. (Обыкновенно неправильно отвечают: «Через 15 суток».)

Часто отвечают: в 1 1/ 2× 5, т. е. в 7 1/ 2минут. При этом забывают, что последний разрез даст два метровых отрубка. Значит, распиливать 5-метровое бревно поперек придется не 5, а 4 раза; на это уйдет всего l 1/ 2 × 4 = 6 минут.

Колхозник ничего не выгадал, а потерял. На вторую половину дороги он употребил столько времени, сколько отняло бы у него все путешествие в город пешком. Значит, он выгадать во времени не может, а должен потерять.

Потерял он 1/ 5того времени, какое нужно, чтобы пройти пешком половину дороги.

Решение этой задачи ясно из следующих выкладок:

24 км в гору и 8 км под гору — 4 ч. 30 м.

8 км в гору и 24 км под гору — 2 ч. 50 м.

Умножив вторую строку на 3, имеем:

24 км в гору и 8 км под гору — 4 ч. 30 м.

24 км в гору и 72 км под гору — 8 ч. 30 м.

Отсюда ясно, что 72 без 8, т. е. 64 километра под гору велосипедист проезжает в 8 ч. 30 м. без 4 ч. 30 м., т. е. в 4 ч. Следовательно, в час он проезжал под гору 64: 4 = 16 километров.