Мартин Гарднер - Математические чудеса и тайны

Перед демонстрацией этого фокуса показывающий должен установить указатель против косточки, на которой сумма очков равна 10, после чего фокус получается автоматически. Такой ящичек не представляет труда сделать самому.

Фокус с фишками

Для демонстрации нужно иметь 6 фишек, на обеих сторонах которых имеются числа. На верхней части рис. 49 показана одна сторона фишек, на нижней части — соответствующая им обратная сторона. Обратим внимание на то, что цифры верхнего ряда выписаны жирными линиями; в нижнем же ряду цифры более тонкие.

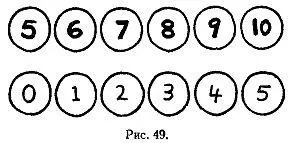
Показывающий просит зрителя перемешать фишки между ладонями, а затем разложить их на столе в два ряда по три фишки в каждом. Пока показывающий стоит, повернувшись спиной, зритель переворачивает три фишки, не сообщая при этом, какие именно. Затем показывающий просит перевернуть еще несколько фишек. После этого зритель берет любую фишку по своему желанию, переворачивает ее и чем-нибудь накрывает (например, игральной картой или монетой — лишь бы не была видна цифра).

То же самое он повторяет еще с двумя фишками.

Теперь на столе три фишки открыты, а три закрыты.

В этот момент показывающий поворачивается к зрителям и называет сумму трех накрытых чисел.

Сущность фокуса состоит в следующем. Прежде чем отвернуться от стола, фокусник бросает беглый взгляд на фишки и запоминает местоположение тех, которые обращены жирными цифрами кверху. После того как зритель перевернет три произвольные фишки, показывающий просит его перевернуть еще несколько фишек.

Он говорит: «Переверните, пожалуйста, вторую фишку в первом ряду и третью фишку в нижнем ряду». Эти фишки должны быть те самые, положение которых он запомнил (т. е. которые вначале находились на местах, занятых фишками, обращенными жирными числами кверху).

Теперь зритель переворачивает три фишки, накрывая каждую из них картой. Показывающий поворачивается к зрителям и производит в уме следующие вычисления: он замечает число фишек, обращенных жирными числами кверху (оно будет равно нулю, одному, двум или трем), и умножает это число на 10. К полученному произведению прибавляет 15. Из этой суммы отнимает сумму трех открытых чисел. Остаток будет равен сумме верхних чисел на трех фишках, накрытых картами [23] Сумма тонких цифр равна 15, а разность между жирной цифрой и тонкой на каждой фишке есть 5. Поэтому если в начале опыта было k фишек с жирными цифрами, то общая сумма всех цифр, открытых зрителям, была равна 15 + 5k . Допустим, что зритель перевернул i фишек с жирными цифрами и j — с тонкими. Показывающий просит перевернуть обратно эти i фишек и еще k — i фишек, остающихся с жирными цифрами, в итоге общая сумма будет 15 + 5 k + 5 j — 5( k — i ) = 15 + 5( i + j ) = 30, причем число фишек с жирными цифрами оказывается равным i + j = 3. Пусть, далее, зритель переворачивает и закрывает р фишек с жирными и q с тонкими цифрами. В результате общая сумма цифр на шести фишках станет 30 — 5p + 5q = 30 — 5 p + 5(3 — p ) = 45–10 p = 10(3 — p )+15, что и дает схему вычислений автора. Можно упростить счет, если не заставлять зрителя перевертывать накрываемые фишки; тогда сумма цифр накрытых фишек получится вычитанием из 30 суммы цифр открытых фишек. ).

В этой и следующей главах мы проследим за ходом развития многих замечательных геометрических парадоксов. Все они начинаются с разрезания фигуры на куски и заканчиваются составлением из этих кусков новой фигуры. При этом создается впечатление, что часть первоначальной фигуры (это может быть часть площади фигуры или один из нескольких изображенных на ней рисунков) бесследно исчезла. Когда же куски возвращаются на свои первоначальные места, исчезнувшая часть площади или рисунок таинственным образом возникают вновь.

Геометрический характер этих любопытных исчезновений и появлений оправдывает причисление этих парадоксов к разряду математических головоломок.

Парадокс с линиями

Все многочисленные парадоксы, которые мы здесь собираемся рассматривать, основаны на одном и том же принципе, который мы назовем «принципом скрытого перераспределения». Вот один очень старый и совсем элементарный парадокс, который сразу объясняет суть этого принципа.

Начертим на прямоугольном листе бумаги десять вертикальных линий одинаковой длины и проведем пунктиром диагональ, как показано на рис. 50.

Посмотрим на отрезки этих линий над диагональю и под ней; нетрудно заметить, что длина первых уменьшается, а вторых соответственно увеличивается.

Разрежем прямоугольник по пунктирной линии и сдвинем нижнюю часть влево вниз, как это показано на рис. 51.

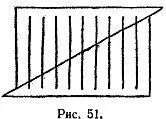
Сосчитав число вертикальных линий, вы обнаружите, что теперь их стало девять. Какая линия исчезла и куда? Передвиньте левую часть в прежнее положение, и исчезнувшая линия появится снова.

Но какая линия стала на свое место и откуда она взялась?

Сначала эти вопросы кажутся загадочными, но после небольшого размышления становится ясным, что никакая отдельная линия при этом не исчезает и не появляется. Происходит же следующее: восемь этих приращений в точности равна длине каждой из первоначальных линий.

Возможно, суть парадокса выступит еще более явственно, если его иллюстрировать на камешках.

Возьмем пять кучек камешков по четыре камешка в кучке. Переместим один камешек из второй кучки в первую, два камешка из третьей во вторую, три из четвертой в третью и, наконец, все четыре камешка из пятой в четвертую. Рис. 52 поясняет наши действия.

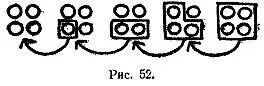
После такой передвижки оказывается, что кучек стало только четыре. Невозможно ответить на вопрос, какая кучка исчезла, так как камешки были перераспределены так, что в каждой из четырех кучек прибавилось по камешку. В точности то же происходит и в парадоксе с линиями. Когда части листа сдвигаются по диагонали, отрезки разрезанных линий перераспределяются и каждая получающаяся при этом линия становится немного длиннее первоначальной.

Исчезновение лица

Перейдем к описанию способов, при помощи которых парадокс с линиями можно сделать более интересным и занимательным. Этого можно, например, достигнуть, заменив исчезновение и появление линий таким же исчезновением и появлением плоских фигур. Здесь особенно подойдут изображения карандашей, папирос, кирпичей, шляп с высокой тульей, стаканов с водой и других вертикально протяженных предметов, характер изображения которых до и после сдвига остается одинаковым. При некоторой художественной изобретательности можно брать и более сложные предметы. Посмотрите, например, на исчезающее лицо на рис. 53.