Льюис Кэрролл - Придирки оксфордского прохожего

Дифференцирование производит на Точку замечательное действие: первая производная зачастую имеет большую влиятельность, чем исходная Точка, а вторая — меньшую просвещённость.

Например, пусть L — это Начальник, а S — Воскресенье; тогда LS — Воскресный Начальник (точка, не имеющая особенной влиятельности). Дифференцируя один раз, получаем LSD [42], влиятельную функцию большой ценности. Сходным образом можно показать, что если взять вторую производную от просвещённой Точки (иначе говоря, возвести её в степень DD [43]), то просвещённость круто понизится. Этот эффект значительно усиливается с добавлением С [44]: в этом случае просвещённость часто полностью пропадает и Точка становится консервативной.

Следует заметить, что где бы ни применялся символ L для обозначения начальника, его следует предварять знаком ± как указанием на то, что его действие иногда положительное, а иногда отрицательное: некоторые точки данного класса приобретают свойство увлекать остальных за собой (таков воинский начальник), а другие отвращать их (такова передовица “Таймс” [45]).

Дать оценку данному Экзаменатору

Пример . На финальном экзамене А проводит 10 партий в вист и выходит с присвоением 3-го разряда; В проводит Экзаменаторов и выходит с присвоением 2-го разряда. Определить ценность Экзаменаторов в терминах виста. Кроме того, дать им оценку в выражениях, на экзамене неприменимых.

Оценить утраты и приобретения

Пример . Дано: записной Подсказчик результата забегов в дерби сообщил о трёх различных предполагаемых победителях трём различным участникам ставок; дано также, что ни одна из названных лошадей не заняла призового места. Найти совокупную для означенных трёх участников ставок утрату 1) денежных средств, 2) самообладания. Найти также и того Подсказчика. Возможно ли последнее в принципе?

Прикинуть направление проводимой линии

Пример . Доказать, что определение линии по Уолтону совпадает с определением по Сальмону, только берутся они за это дело с противоположных концов. Считая, что такая линия разделена методом Фроста, дать ей справедливую оценку по Прайсу [46].

Конец (т. е. «произведение крайних членов») оправдывает (т. е. «приравнивается к») середину [47].

К этому Предложению в силу очевидных причин пример не прилагается.

Продолжить данный ряд

Пример . А и В, примкнувшие соответственно к Четвёрке и Пятёрке, занимают столько же постов, сколько всегда находятся в распоряжении Шестёрки и Семёрки. Найти вероятное количество чтений, проведённых А и В, пока Восьмёрка на подходе.

Перейдём к иллюстрации этого торопливого наброска Динамики Партийной Горячки. Предложим здесь одну замечательную Задачу, от решения которой зависит вся теория Представления, а именно: «Удалить данную Касательную от данного Круга, а взамен привести в соприкосновение с ним другую».

Чтобы решить поставленную задачу алгебраическими средствами, лучше всего представить такой круг в тангенциальных координатах, где один тангенс задают линии WEG и WH, а другой — линии WH и GH [48]. Когда этот шаг будет выполнен, станет видно, что удобнее спроецировать линию WEG в бесконечность. Полностью эту процедуру мы здесь не даём, поскольку она требует введения множества путанных детерминантов.

Удалить данную Касательную от данного Круга, а взамен привести в соприкосновение с ним другую.

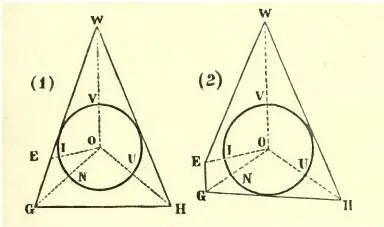
Пусть UNIV будет Большим Кругом, центр которого находится в точке О (а буква V, разумеется, лежит в верхней точке окружности) [49], и пусть WGH — это треугольник, две стороны которого, WEG и WH, соприкасаются с нашим кругом, а GH (называемая свободомыслящими математиками «основанием»), с ним не соприкасается (см. фиг. 1). Требуется нарушить соприкасаемость WEG, а вместо неё привести в соприкосновение с кругом GH.

Пусть на точку I приходится наибольшая частота озаряемости по сравнению с остальной частью данного круга, тогда как на точку E — максимум просвещённости [50]по сравнению с остальной частью треугольника. (Понятно, что абсолютная величина этого максимума изменяется обратно квадрату расстояния точки Е от О.)

Пусть WH абсолютно фиксирована и всегда остаётся в контакте с кругом, и пусть также фиксировано направление OI.

Теперь, пока WEG сохраняет совершенно прямой курс, GH не имеет возможности войти в соприкосновение с кругом, но если сила озарения, действующая вдоль OI, вынудит WEG отклониться (фиг. 2), то последует её излом и поворот GH; WEG перестанет касаться круга, а GH немедленно придёт с ним в соприкосновение. Доказательство окончено.

Теория, привлечённая для решения вышепредложенной Задачи, в настоящее время вызывает много споров, и от сторонников её требуют показать, где та фиксированная точка , или locus standi, в которой они предполагают выполнить необходимый излом. Чтобы прояснить этот пункт, мы должны обратиться к греческому оригиналу и напомнить нашим читателям, что надёжная точка , или locus standi, в данном случае есть ἄρδις (или ἅρδις [51]в соответствии с современным употреблением), и поэтому не может быть приписана WEG. В ответ на это недруги настаивают, что в подобных нашему случаях одно только словечко нельзя рассматривать как удовлетворительное объяснение, даже и ἁρδέως [52].

Также следует отметить, что обсуждаемый здесь излом является всецело следствием просвещённости, поскольку точки, озаряемые так часто, что и впрямь начинают сходить за φώς [53], имеют привычку держаться одна от одной подальше; и это при том, что если смотреть в корень, то ясно ведь, что радикальная сила [54]данного понятия заключается в таких его атрибутах как «стремящийся к единению», или «дружественно настроенный». Но читатель сам найдёт тому у Лиддела и Скотта [55]замечательную иллюстрацию, из которой становится ясным одно существенное условие: такое чувство можно питать только φοράδην [56], и точка, его питающая, относится к роду σκότος, отчего и получается, что она, по крайней мере номинально, не может быть отнесена к просвещённым.