Александра Арсентьева - Когда любовь стремится к бесконечности. Роман

Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала, затем,, …,, ….

То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

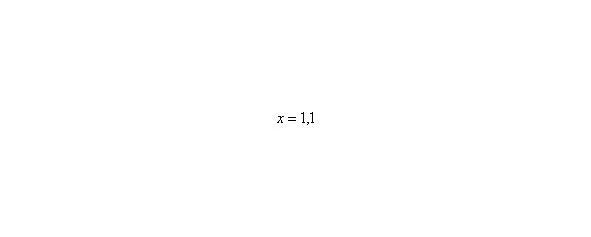
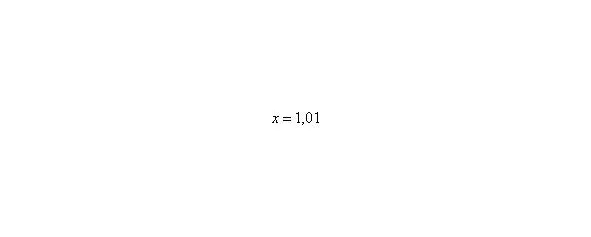
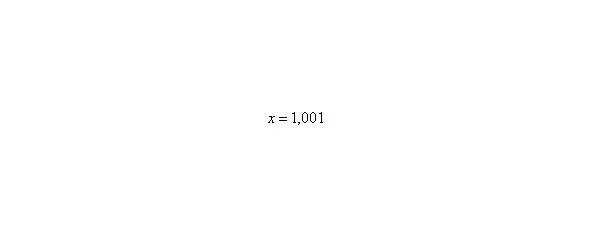
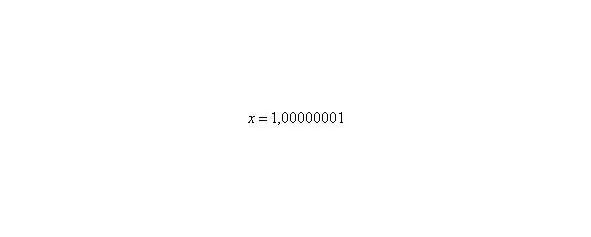
Решаем вышерассмотренный пример. Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

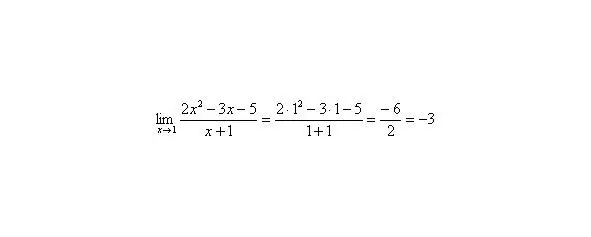
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью – мой любимый, кстати:

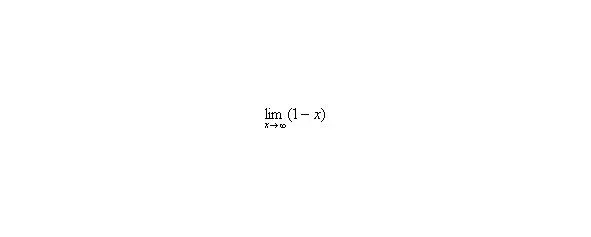
Студенты захихикали, рассматривая на ее тонкой руке изящный браслет со знаком бесконечности.

– Это мой талисман, – она смутилась, поправляя любимое украшение.

– Разбираемся, что такое? Это тот случай, когда неограниченно возрастает, то есть: сначала, потом, потом, затем и так далее до бесконечности.

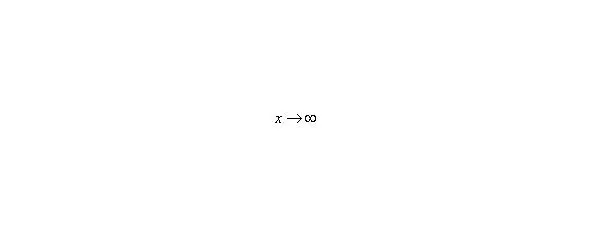
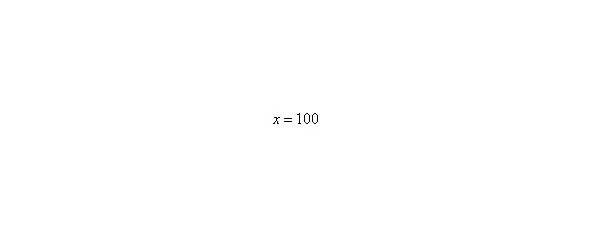
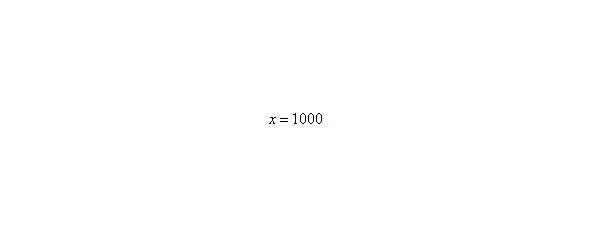
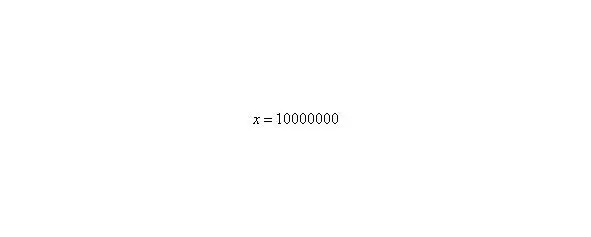
А что в это время происходит с функцией?

,,,…

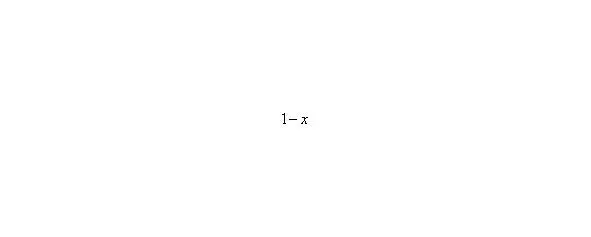
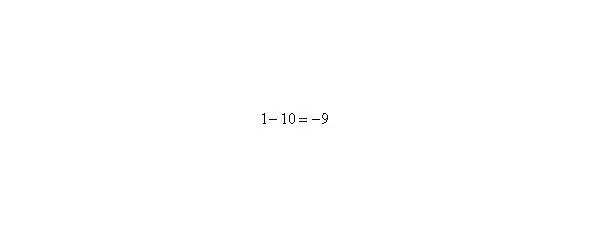
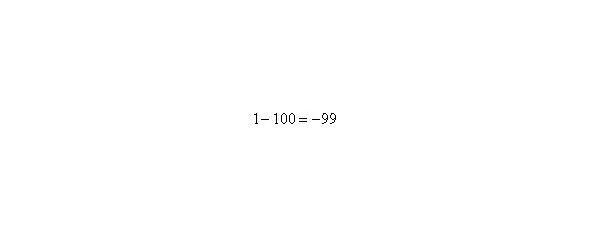
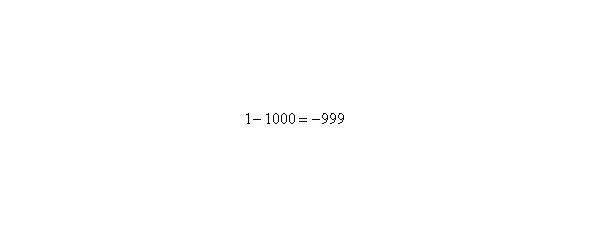
Итак: если, то функция стремится к минус бесконечности:

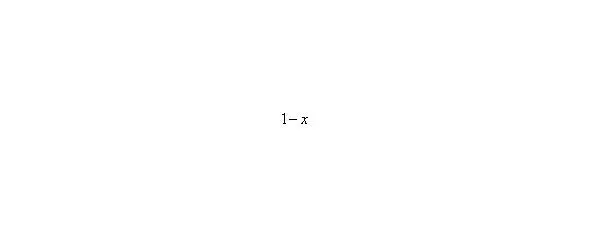
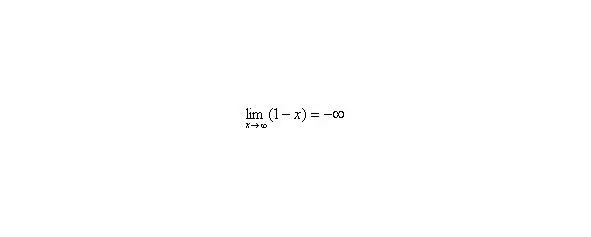
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.

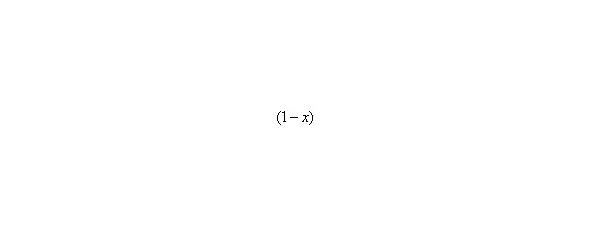
– И незнакомца в подарок, который преподнес Вам браслет! – пошутил один из симпатичных и высоких парней, некто Ментор.

– Вы что-то об этом знаете? – встрепенулась Афродита.

– Не выдавайте себя так глупо, мадам, – улыбнулся Ментор.

– Мы знаем только то, что Вы нам преподаете. А еще я готов признать тот факт, что Вы прекрасны.

Афродита нахмурилась, приготовившись продолжать объяснение пределов.

– Еще один пример с бесконечностью:

Опять начинаем увеличивать до бесконечности, и смотрим на поведение функции:

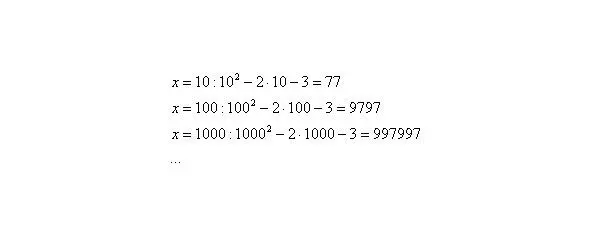
Вывод: при функция неограниченно возрастает:

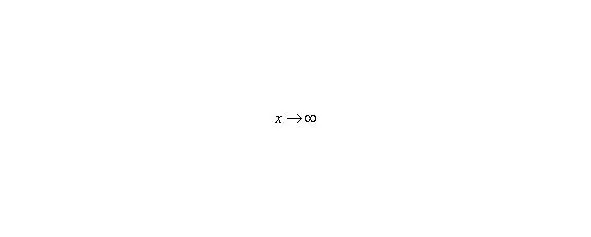
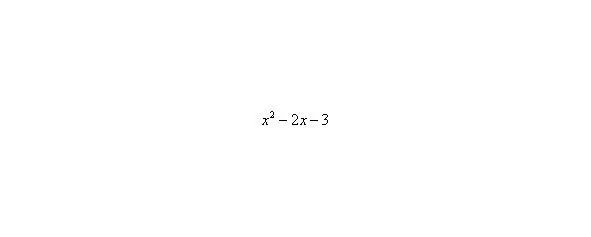
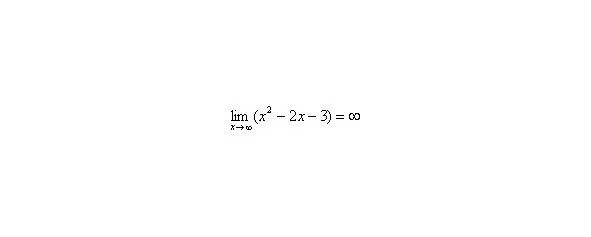
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

,,,,,,,,,

Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.

В том случае, если, попробуйте построить последовательность,,. Если, то,,.

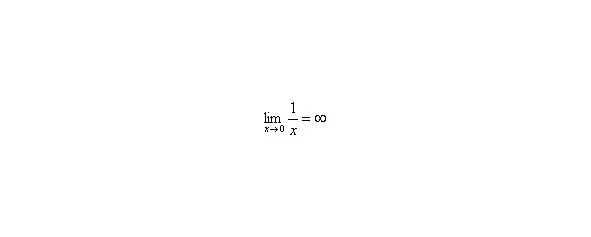
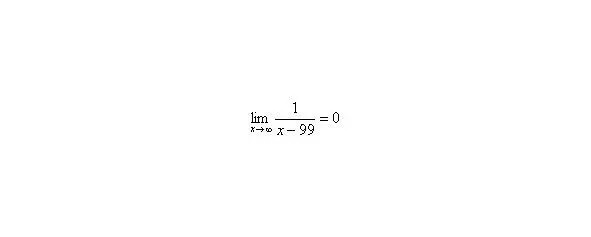
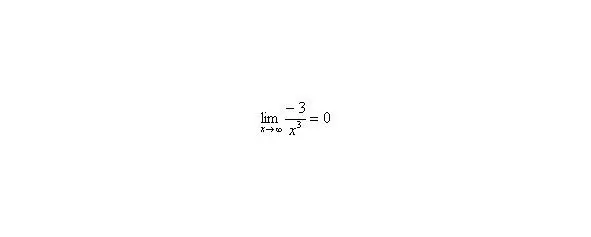
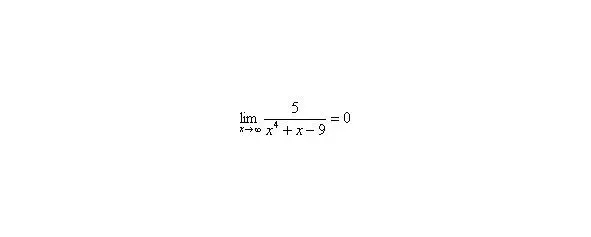
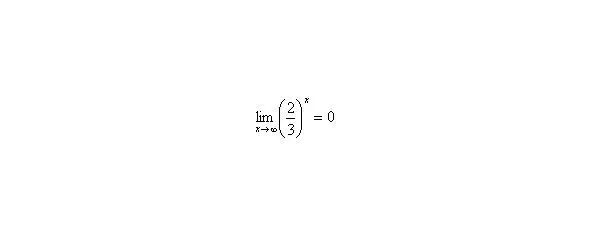
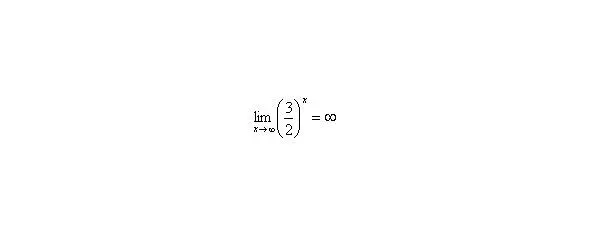
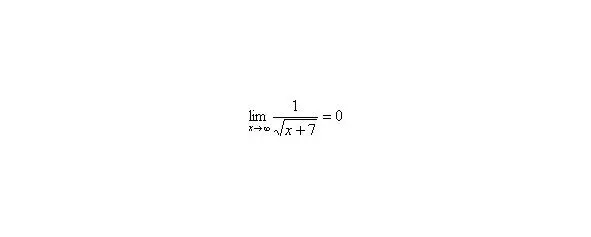
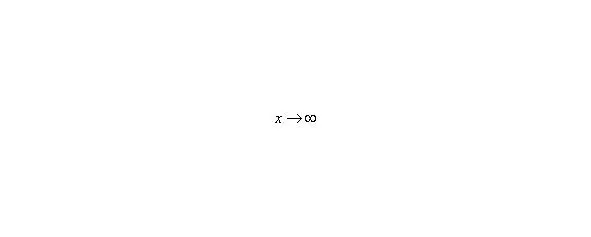
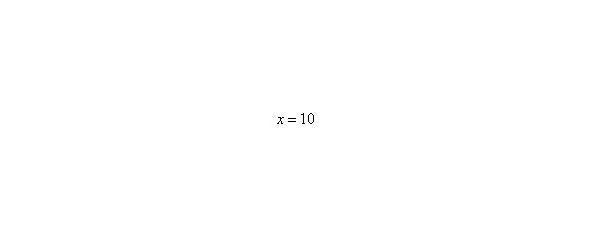
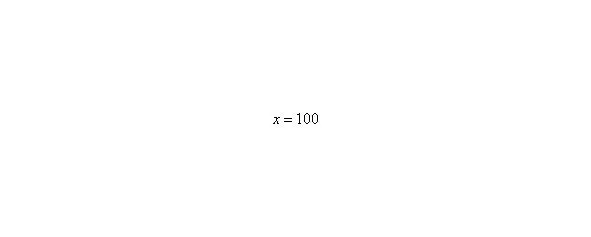
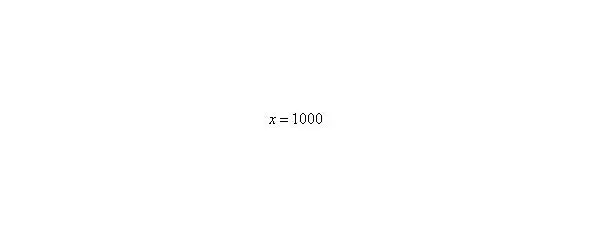
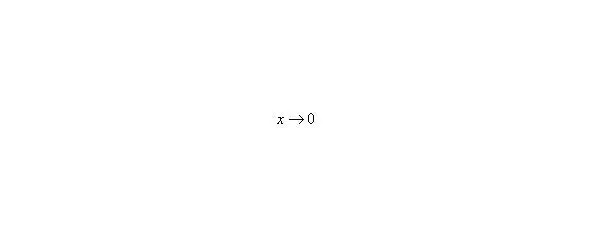
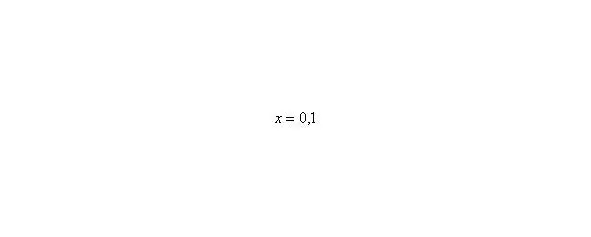
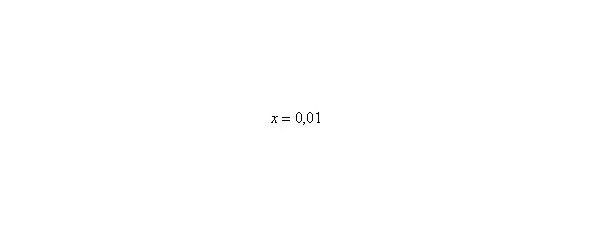
Примечание : строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.