Александра Арсентьева - Когда любовь стремится к бесконечности. Роман

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом:, то все равно, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

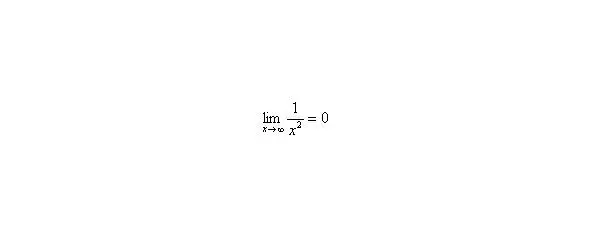
2) Вы должны понимать и сразу решать простейшие пределы, такие как,, и т. д.

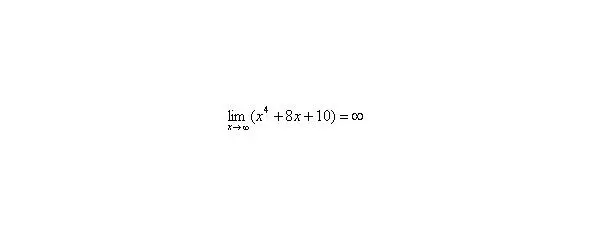
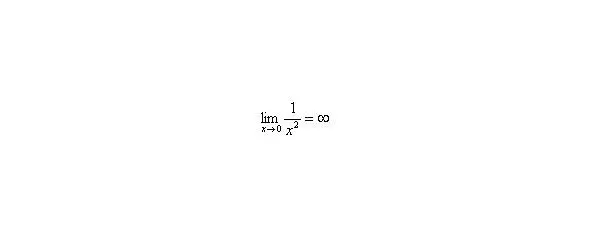
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.

Пределы с неопределенностью вида и метод их решения

Сейчас мы рассмотрим группу пределов, когда, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

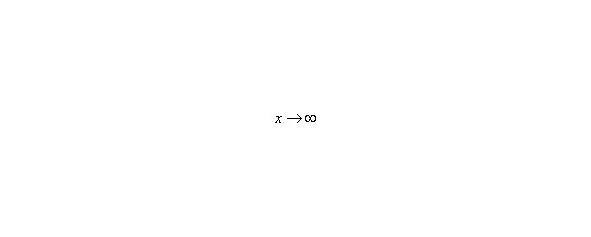
Пример:

Вычислить предел

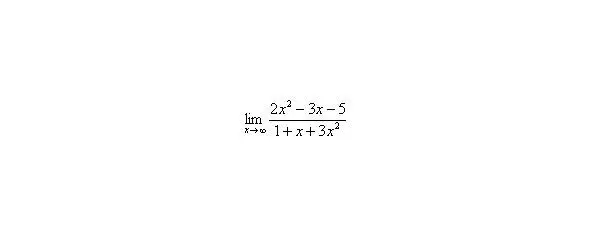
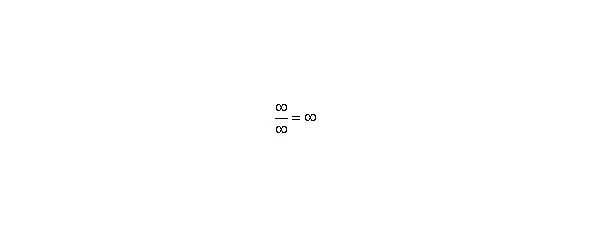
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида. Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

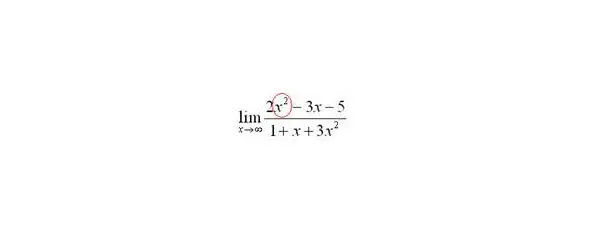
Теперь смотрим на знаменатель и тоже находим в старшей степени:

Старшая степень знаменателя равна двум.

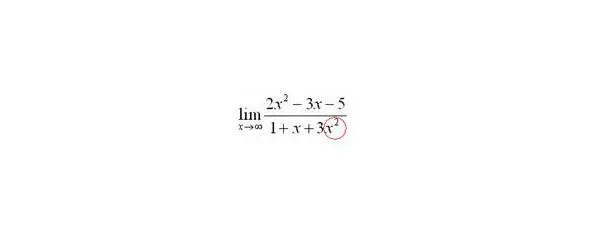
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

Разделим числитель и знаменатель на

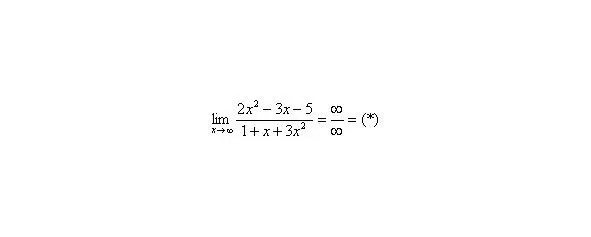
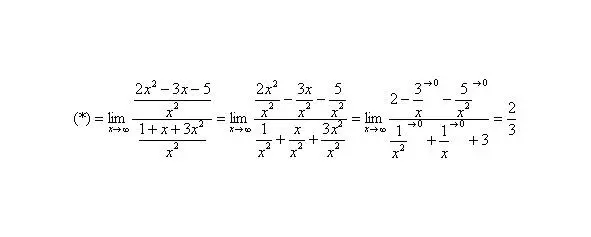
Вот оно как, ответ, а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

Для пометок лучше использовать простой карандаш.

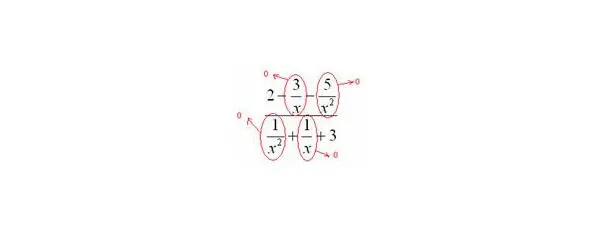
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 2

Найти предел

Снова в числителе и знаменателе находим в старшей степени:

Максимальная степень в числителе: 3

Максимальная степень в знаменателе: 4

Выбираем наибольшее значение, в данном случае четверку.

Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на.

Полное оформление задания может выглядеть так:

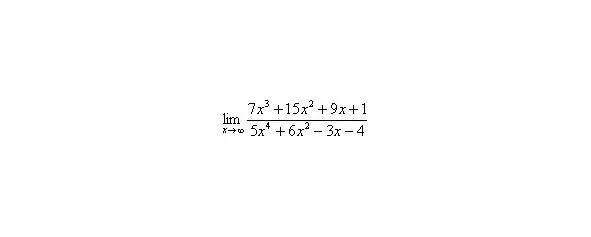
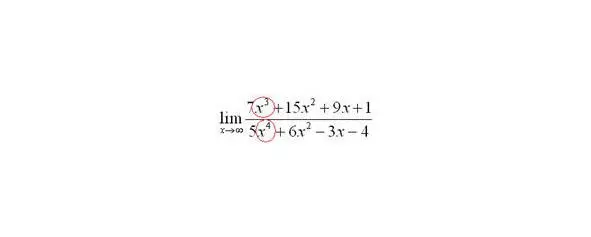
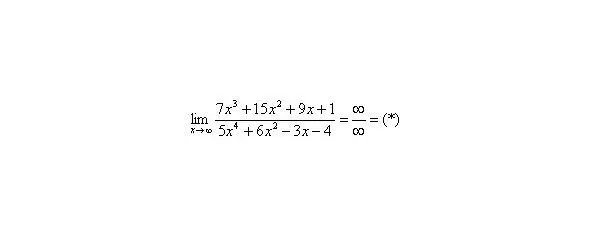
Разделим числитель и знаменатель на