Александра Арсентьева - Когда любовь стремится к бесконечности. Роман

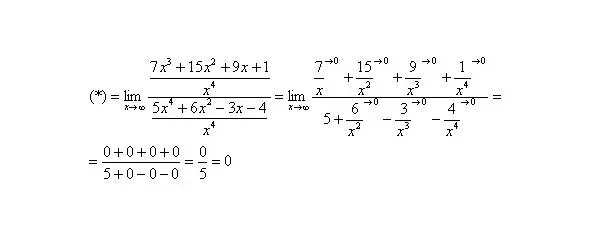
Пример 3

Найти предел

Максимальная степень «икса» в числителе: 2

Максимальная степень «икса» в знаменателе: 1 (можно записать как)

Для раскрытия неопределенности необходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:

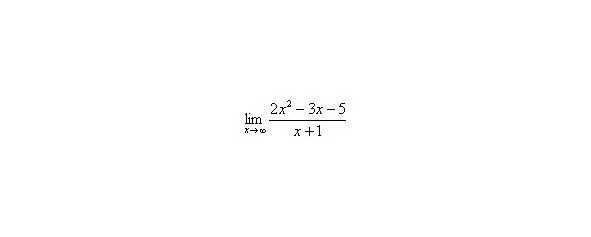
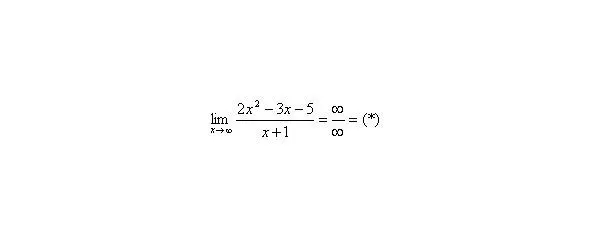
Разделим числитель и знаменатель на

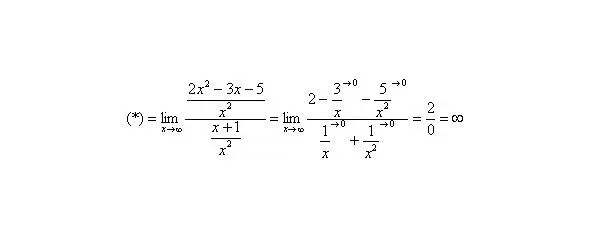
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число , ноль или бесконечность.

Пределы с неопределенностью вида и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу .

Пример 4

Решить предел

Сначала попробуем подставить -1 в дробь:

В данном случае получена так называемая неопределенность.

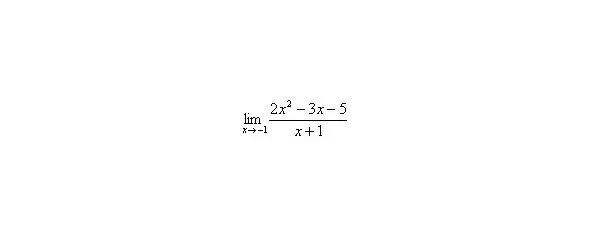
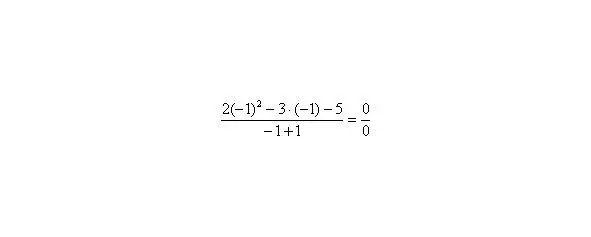
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Математические формулы и таблицы. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

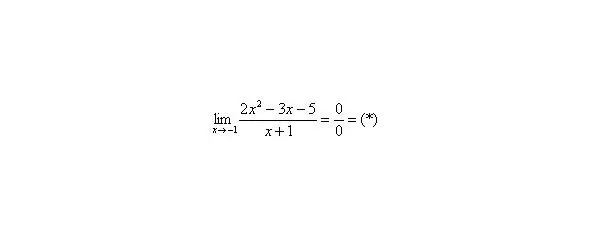
Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него:.

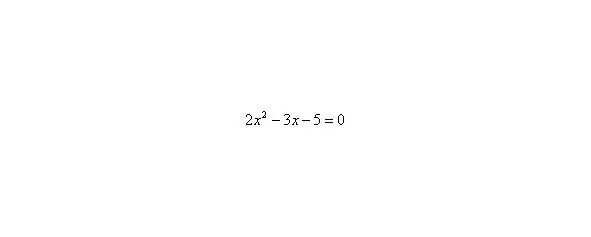
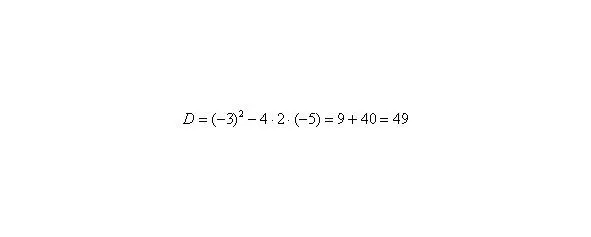
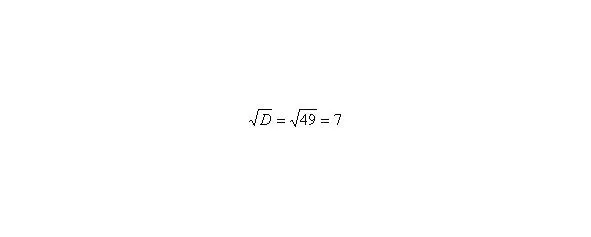
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

!Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни:

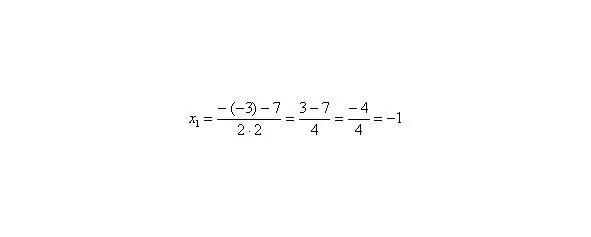
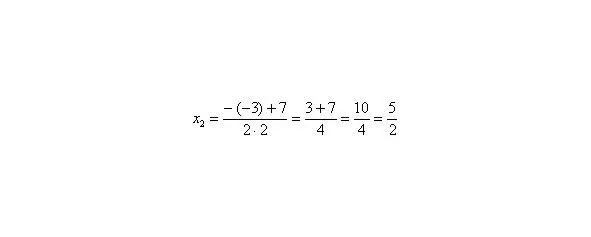
Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.

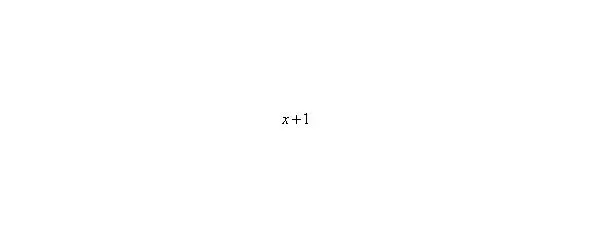
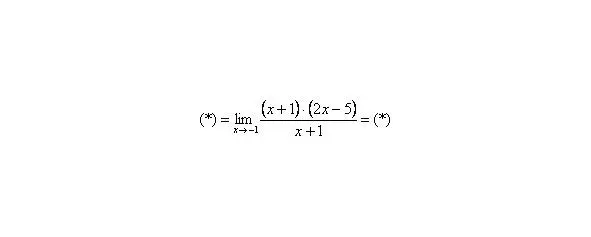
Очевидно, что можно сократить на:

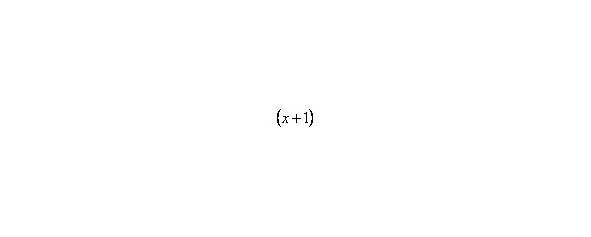
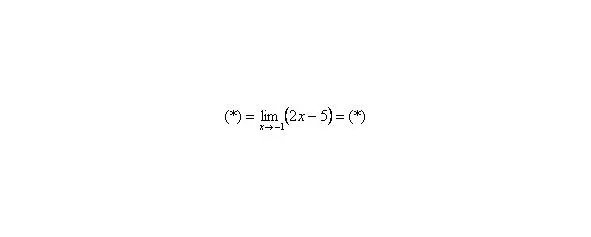
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

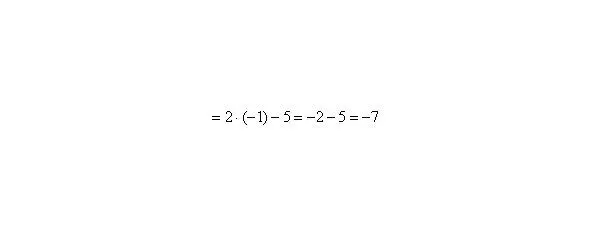
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

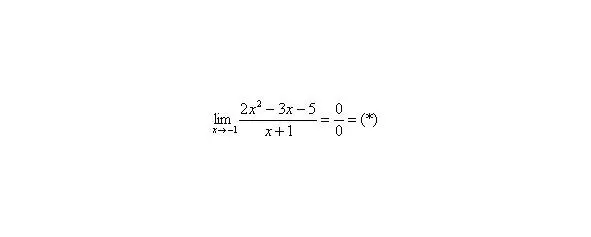
Разложим числитель на множители.