Виктор Попенко - Секретные инструкции спецназа ГРУ

Крутизна ската определяется по величине заложения (расстояния) между основными горизонталями. Чем ближе друг к другу на карте расположены горизонтали, тем скат круче; чем больше расстояние между соседними горизонталями, тем скат положе. При одной и той же высоте сечения в зависимости от изменения крутизны ската меняется и величина заложения.

Крутизну ската можно определить по шкале заложений, помещаемой под южной стороной рамки карты. Для этого надо измерить циркулем расстояние между двумя смежными сплошными горизонталями (рис. 3)и приложить циркуль к шкале так, как показано на рис. 3а. Отсчет внизу на шкале против ножки циркуля укажет крутизну ската в градусах. В нашем примере между точками « а » и « б » она равна 1°. На крутых скатах крутизну определяют по утолщенным горизонталям. Раствор ножек циркуля устанавливают между двумя соседними утолщенными горизонталями, a затем, приложив его ножки к графику, находящемуся справа, как показано на этом же рисунке, определяют крутизну ската. В нашем примере между точками « в » и « г » она равна 10°.

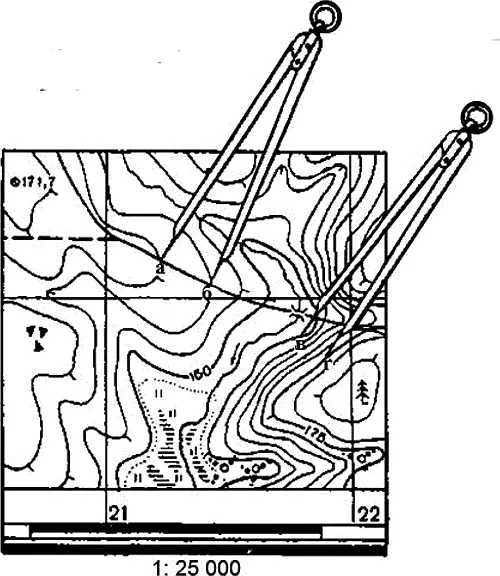
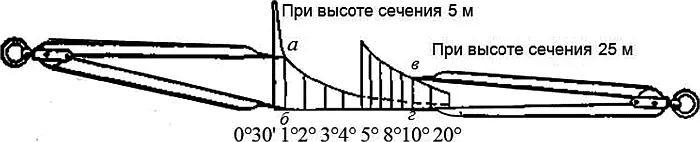
К рис. 3, 3а.Определение крутизны ската по шкале заложений

Взаимная видимость точек определяется путем внимательного изучения рельефа и местных предметов, расположенных по направлению наблюдения. Простейшим способом определить взаимную видимость точек можно путем сопоставления их высот (рис. 4). Для этого по линии пункт наблюдения (ПН) — цель (Ц) выявляют возможное укрытие (У) и по горизонталям определяют абсолютные высоты пункта наблюдения ПН, укрытия У и цели Ц. Если высота укрытия больше высоты ПН и высоты Ц, то цель не видна (рис. 4, поз. «a»), a если меньше — цель видна (рис. 4, поз. «б»). В сомнительных случаях эту задачу решают путем построения треугольника. Для этого соединяют на карте точки ПН и Ц прямой линией и отмечают укрытие У (рис. 4, поз. «в»); определяют абсолютные высоты ПН, У и Ц; высоту самой низкой точки принимают за нуль и относительно нее определяют превышение двух других точек; в нашем примере нулевой является высота цели, укрытие выше нее на 10 м, a пункт наблюдения на 50 м; полученные превышения откладывают в произвольном масштабе от соответствующих точек по перпендикулярам к линии НП — Ц (на рис. 4, 1 см на карте соответствует 20 м на местности). Точки на перпендикулярах соединяют прямой линией (луч зрения). Если эта прямая пройдет ниже нулевой точки, как в нашем примере, то цель будет видна.

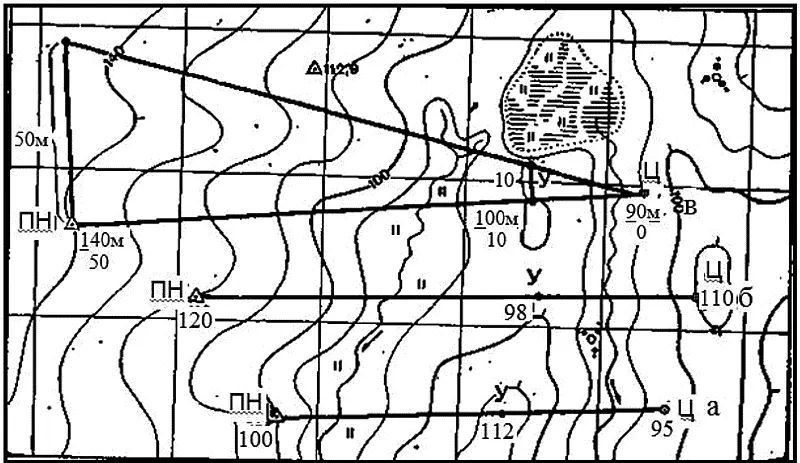
Рис. 4Определение видимости точек: а, б — сопоставлением высот; в — построением треугольника

Нанесение на карту целей, ориентиров или других объектов по их известным координатам. Допустим, что цель (пулемет) на местности расположена в точке, ничем не отмеченной на карте, но известны ее координаты: x = 15175; y = 52420. Для нанесения ее на карту необходимо определить квадрат, в котором она находится. Две первые цифры у координат х и у (десятки и единицы километров) показывают, что цель находится в квадрате 1552 (15 — горизонтальная линия, 52 — вертикальная линия). В квадрате 1552 отложим по вертикальным линиям сетки 175 м, нанесем точки и соединим их прямой. На этой прямой где-то находится цель. По прочерченной линии вправо от вертикальной линии сетки, имеющей надпись 52, отложим отрезок 420 м и нанесем точку. Полученная точка и будет местом расположения цели на карте (в нашем примере — пулемет) (рис. 5).

Определение по карте координат точек местности и объектов (целей). Координатами называются угловые или линейные величины, определяющие положение точки на какой-либо поверхности или в пространстве. При определении координат точек (целей) на местности по карте широко применяются плоские прямоугольные координаты. Плоские прямоугольные координаты (рис. 5а) — линейные величины, определяющие положение точек на плоскости относительно установленного начала координат. В общем случае за начало координат принимается точка пересечения двух взаимно перпендикулярных линий (оси координат). Оси X и Y в геодезии расположены совсем не так, как в математике: вертикальная ось (направленная на север) здесь называется осью икс (X), а горизонтальная — осью игрек (Y). Положение точки М определяется отрезками осей 0а и 0б или, что то же самое, кратчайшими отрезками (перпендикулярами) от определяемой точки до соответствующих осей координат.

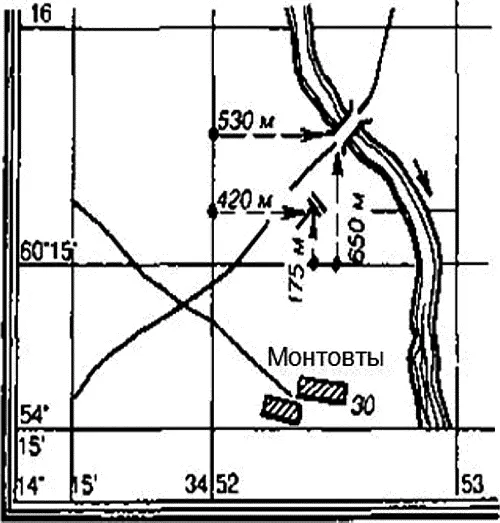
Рис. 5.Определение координат по карте и нанесение точек на карту по известным координатам

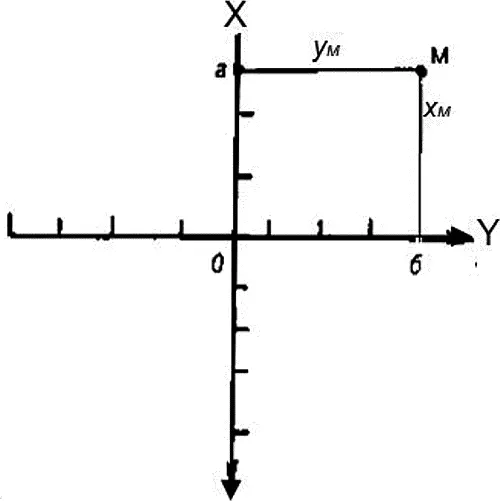
Рис. 5аОси прямоугольных координат

Значения величин X считаются положительными вверх от линии 0Y (оси Y) и отрицательными вниз от нее. Значения величин Y считаются положительными вправо (восточнее) от линии 0Х (оси X) и отрицательными влево от нее (западнее этой линии).

На топографических картах система плоских прямоугольных координат дается в виде сетки взаимно перпендикулярных линий, проведенных на равных расстояниях одна от другой и образующих сетку квадратов, которая называется координатной или километровой сеткой. Чтобы указать приближенно местоположение какого-либо местного предмета (объекта, цели), достаточно указать квадрат сетки, в которой он расположен.

Квадрат всегда указывается подписями километровых линий, пересечением которых образован его юго-западный (нижний левый) угол. При указании квадрата надо придерживаться обязательного правила: сначала назвать две цифры, подписанные у горизонтальной линии, т. е. координату X, а затем две цифры, подписанные у вертикальной линии, т. е. координату Y. При этом цифры пишутся и произносятся слитно, без разделения их на Х и Y, например, «девяносто ноль два (9002)», «восемьдесят восемь ноль четыре (8804)».

Определение по карте координат точек производится в следующем порядке. Определяют расстояния (по перпендикуляру) в метрах сначала от горизонтальной линии (нижней стороны квадрата), а затем от левой вертикальной линии (левой стороны квадрата), в котором находится эта точка. Полученные расстояния в метрах прибавляют к значениям координат линий в километрах, от которых измерялось расстояние до точки: расстояние от нижней горизонтальной стороны квадрата прибавляют к координате X, а расстояние от левой вертикальной стороны квадрата — к координате Y. Полученные величины и будут координатами точки. На рис. 5даны сокращенные координаты моста: x = 15650; y = 52530. Полные координаты точки: x = 6015650; y = 3452530.