Василий Кандинский - О духовном в искусстве. Ступени. Текст художника. Точка и линия на плоскости

Кроме того, так как точка здесь является сложным единством (ее размер + ее форма), то легко можно себе представить, какой взрыв звуков произойдет от все большего скопления точек на плоскости, а также разовьется в случае их идентичности, и как распространится последующее развитие этого взрыва, если в дальнейшем точки окажутся брошенными на плоскость различными и все более нарастающими несоответствиями размера и формы.

В другом несмешанном царстве – в природе – часто происходит скопление точек, и это всегда целенаправленно и органично необходимо. Эти природные формы в действительности являются маленькими пространственными телами и находятся в таком же соотношении к абстрактной (геометрической) точке, как и живописные. Однако можно весь «мир» рассматривать как одну замкнутую в себе космическую композицию, которая, в свою очередь, состоит из бесконечных, самостоятельных, также замкнутых в себе и все уменьшающихся композиций, в большей или меньшей степени состоящих из тех же точек, и при этом точка, в свою очередь, возвращается к своей первоначальной геометрической сущности. Это комплексы геометрических точек, которые в различных закономерных сочетаниях парят в геометрической бесконечности. Самые маленькие, замкнутые в себе, чисто центробежные формы мы видим невооруженным глазом как малосвязанные между собой точки. Так выглядит семя. Раскрыв красивый, гладко отполированный, похожий на слоновую кость маковый шар (в конце концов, он является самой большой шарообразной точкой), мы обнаруживаем в этом теплом ядре композиционно планомерно выстроенное множество холодных серо-голубых точек, которые содержат в себе еще покоящуюся силу прорастания; то же происходит и с живописной точкой.

В природе такие формы иногда возникают в процессе расчленения и распада вышеназванного комплекса, можно сказать, как возвращение к прообразу, к первичному геометрическому состоянию. Если пустыня есть море песка, которое состоит исключительно из точек, тогда непреодолимо мятежная способность этих «мертвых» точек к передвижению не случайно действует пугающе.

В природе точка, так же как и в живописи, является обращенным внутрь себя, полным возможностей существом (рис. 5 и 6).

Рис. 5. Скопление звезд в созвездии Геркулес (Newcomb-Engelmann›s «Popul. Astronomie». Leipzig, 1921. S. 294)

Точка и линия на плоскости

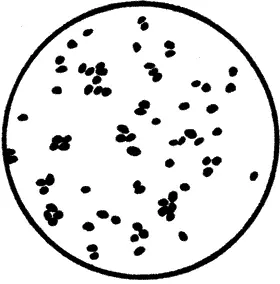
Рис. 6. Образование нитритов. Увеличение в 1000 раз («Kultur der Gegenwart». Т. III, Abtlg. IV, 3. S. 71)

Точки встречаются во всех искусствах, и их внутренняя сила, вероятно, все более будет осознаваться художниками. Нельзя недооценивать внутреннего значения точки.

В скульптуре и архитектуре точка является результатом пересечения нескольких плоскостей, она, с одной стороны, – вершина пространственного угла, а с другой – опорная точка образования этих плоскостей. Плоскости ею управляются и из нее развиваются. В готических зданиях точки акцентируются резкими обострениями и нередко подчеркнуты пластически, в китайских это достигается благодаря кривой, ведущей к точке, – становятся внятными короткие, точные упоры, как переход пространственной формы к растворению в окружающем здание воздушном пространстве. Именно в такого вида постройках предполагается сознательное применение точки. Так как она планомерно распределяет и композиционно восходит к самой вершине устремленных вверх масс. Вершина = точка (рис. 7 и 8).

Рис. 7. Ling-ying-si, внешний портал. («China» v. Bernd Melchers, 2 Bd. Folkwang Vlg., Hagen i. W., 1922)

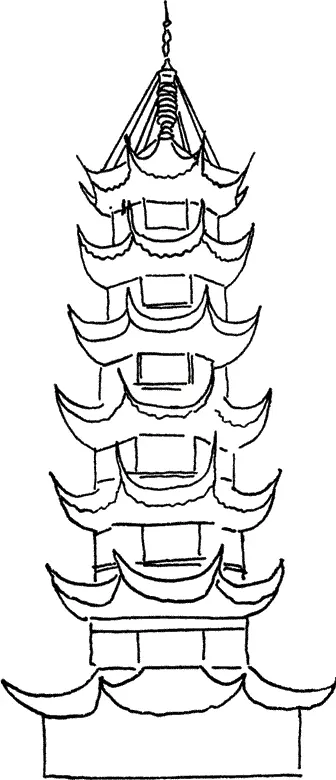
Рис. 8. «Пагода Красоты Дракона» в Шанхае (1411)

Уже в классическом балете есть «пуанты», терминологически происходящие от слова «острие». Быстрый бег на кончиках пальцев оставляет после себя точки на полу. Артист балета использует точку при прыжке таким образом, что головой обозначает точкой верх, а становясь на ступню и соприкасаясь с полом – низ. Прыжок в высоту в новом танце можно в некоторых случаях противопоставить «классическому» балетному прыжку – прежний изображает непосредственно вертикаль, а «современный», напротив, иногда образует пятиугольную плоскость с пятью вершинами – голова, две руки, два мыска, причем десять пальцев образуют десять маленьких точек (рис. 9). Застывшую, короткую неподвижность также можно воспринимать как точку. Так, активное и пассивное пунктирование связано с музыкальной формой точек.

Рис. 9. Прыжок танцовщицы Палукки

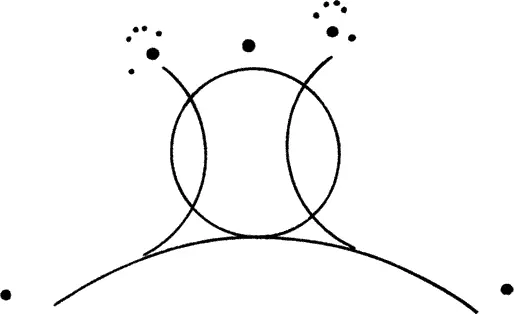
Рис. 10. Графическая схема к фотографии (рис. 9)

Кроме уже упомянутых ударов в литавры и треугольник точки в музыке могут по-разному производиться различными инструментами (особенно это касается ударных инструментов), например, рояль осуществляет законченные композиции исключительно благодаря сопоставлению и последовательности звуковых точек [142].

Рис. 11. V симфония Бетховена (первые такты)

То же самое, переведенное в точки

То же самое, переведенное в точки

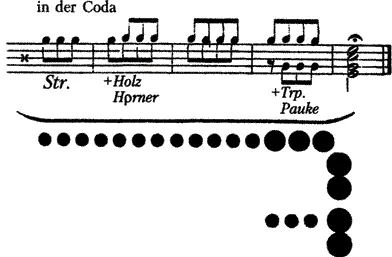
То же самое, переведенное в точки

Рис. 11. Тема 2, переведенная в точки [143]

В специальной области живописи, в графике , точка развивает свои самостоятельные силы с особой ясностью. Материальный инструмент предоставляет этим силам много различных возможностей, что увеличивает разнообразие форм и размеров, а также превращает точки в бесчисленные, по-разному звучащие существа.