Василий Кандинский - О духовном в искусстве. Ступени. Текст художника. Точка и линия на плоскости

Среди прямых линий мы различаем три типичных вида, все прочие прямые будут лишь их разновидностями.

1. Самая простая форма прямой – горизонталь . В человеческом представлении она соответствует линии или плоскости, на которой человек стоит или по которой он движется. Итак, горизонталь – это холодный несущий базис, плоскость которого может быть продолжена в любом из направлений. Холодность и плоскостность являются основным звучанием этой линии. Она может быть обозначена как самая малая форма бесконечной холодной возможности движения (die knappste Form der unendlichen kalten Bewegungsmöglichkeit).

2. Этой линии в полной мере внешне и внутренне противостоит идущая к ней под прямым углом вертикаль , в которой плоскостность заменяется высотой, а значит холод – теплом. Таким образом, вертикаль является самой малой формой бесконечной теплой возможности движения (die knappste Form der unendlichen warmen Bewegungsmöglichkeit).

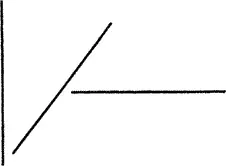
Рис. 14. Основные типы геометрической прямой

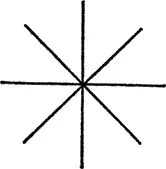
Рис. 15. Схема основных типов прямых линий

3. Третьим типичным видом прямой линии является диагональ , которая, будучи проведена под одинаковым углом к двум предыдущим прямым, обладает свойствами их обеих, что и определяет ее внутреннее звучание: равномерное объединение холода и тепла. Итак, она является самой малой формой бесконечной холодно-теплой возможности движения (die knappste Form der unendlichen kaltwarmen Bewegungsmöglichkeit) (рис. 14 и 15).

Эти три вида линий – самые чистые формы прямых, отличающихся друг от друга температурой :

Все остальные прямые в большей или меньшей степени являются отклонениями от диагонали, в большей или меньшей степени склонны к холоду или теплу, что и определяет их внутреннее звучание (рис. 16).

Так, при пересечении этих линий в одной точке возникает звезда из прямых линий.

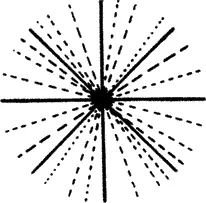
Рис. 16. Схема отклонений в температуре

Эта звезда может становиться все плотнее и плотнее, так что место пересечения создающих ее прямых образует более плотную середину, в которой возникает и кажется растущей точка. Она является осью, вокруг которой линии могут двигаться и, в конце концов, перетекать друг в друга – так рождается новая форма: плоскость с четкой конфигурацией круга (рис. 17 и 18).

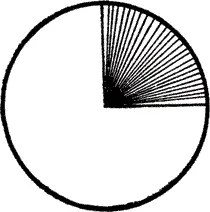
Рис. 17. Уплотнение

Рис. 18. Круг как результат уплотнения

Здесь следует лишь мимоходом заметить, что в этом случае мы имеем дело с особым свойством линии – с силой образования ею плоскостей. Внешне эта сила выражается в виде своеобразной лопаты, которая производит плоскость движением своей острой части по земле. Но линия может образовывать и другой вид плоскости, о чем я буду говорить позднее.

Разница между диагоналями и прочими диагональными линиями, которые по праву можно было бы назвать свободными прямыми , проявляется в различии их температур, из-за которого свободные прямые никогда не смогут достичь равновесия между теплом и холодом.

При этом свободные прямые могут располагаться на данной плоскости или в общем центре (рис. 19), или вне центра (рис. 20), в связи с чем они делятся на два класса:

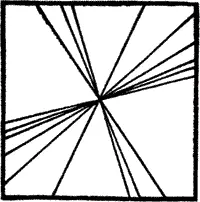
Рис. 19. Центральные свободные прямые

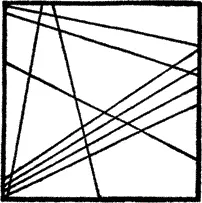
Рис. 20. Ацентральные свободные прямые

4. Свободные прямые (находящиеся вне равновесия):

а) центральные и

б) ацентральные.

Ацентральные свободные прямые обладают особой способностью, которая создает возможность возникновения определенных параллелей с «пестрыми цветами» и которая отличает их от черного и белого. Особенно желтый и синий цвета несут в себе различные напряжения – напряжения выступать вперед и уходить назад. Чисто схематические прямые (горизонталь, вертикаль, диагональ, и в особенности первая и вторая) развивают свои напряжения на плоскости, не проявляя тенденции удаляться от нее.

У свободных, и особенно у ацентральных, прямых мы замечаем ослабленную связь с плоскостью: они в меньшей степени сливаются с нею, а иногда кажется, будто бы они пронзают ее. Так как эти линии утратили элемент покоя, то они оказываются наиболее удаленными от впивающейся в плоскость точки.

На ограниченной плоскости локальная взаимосвязь возможна лишь тогда, когда линия свободно располагается на ней, другими словами, когда линия не касается внешних границ плоскости, о чем более подробно пойдет речь в главе «Основная плоскость».

В любом случае существует определенное родство напряжений ацентральных свободных прямых и «пестрых» цветов. Естественная взаимосвязь «рисуночных» и «живописных» элементов, которую мы сегодня до известных пределов можем уловить, имеет неоценимо большое значение для будущего учения о композиции. Только этим путем могут быть проведены планомерные, точные эксперименты в области конструкций, и коварный туман, в котором мы сегодня обречены блуждать при лабораторной работе, станет, безусловно, более прозрачным и менее удушливым.

Если схематические прямые – в первую очередь горизонталь и вертикаль – проверить на цветовые свойства, то логично напрашивается сравнение с черным и белым . Так же как эти два цвета (которые коротко называли «нецветами», а сегодня не очень удачно называют «непестрыми» цветами) являются молчащими цветами, так и обе вышеназванные прямые являются молчащими линиями. И здесь, и там звучание доведено до минимума: молчание или едва слышный шепот и покой. Как черное и белое расположены вне цветового круга [147], так и горизонтали и вертикали занимают особое место среди линий, в центральном положении они неповторимы и поэтому одиноки. Если мы черное и белое рассмотрим с точки зрения температуры, то скорее белое, а не черное является теплым, а абсолютно черное внутренне будет непременно холодным. Не случайно горизонтальная цветовая шкала проходит от белого цвета к черному (рис. 21).