Василий Кандинский - О духовном в искусстве. Ступени. Текст художника. Точка и линия на плоскости

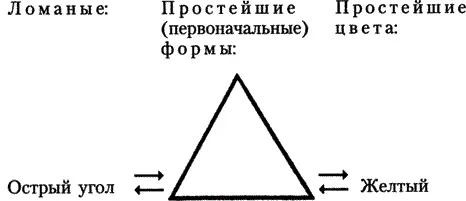
Рис. 30

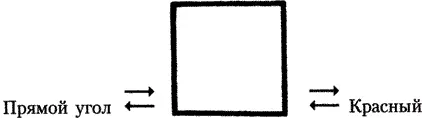
Рис. 31

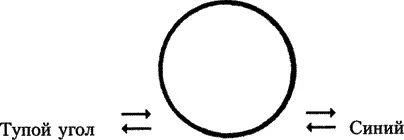
Рис. 32

Если эти и представленные выше параллели верны, то в результате этого сравнения можно сделать вывод: звуки и свойства составляющих формируют в отдельных случаях такую сумму свойств, которая ими не перекрывается. Похожие факты известны и в других науках, например в химии: разложенная на составляющие сумма не всегда получается при обратном составлении [154]. Возможно, в подобных случаях мы имеем дело с неизвестным законом, неясное лицо которого вызывает замешательство.

А именно:

Так, сумма создала бы недостающий член составляющих, необходимый для равенства. Таким способом из суммы получались бы ее составляющие – линии из плоскости, и наоборот. Художественная практика придерживается этого так называемого правила, благодаря которому черно-белая живопись, состоящая из линий и точек, при введении плоскости (или плоскостей) получает бросающееся в глаза равновесие: легкий вес требует в противовес более тяжелого. Возможно, даже в еще большей степени эту необходимость можно наблюдать в полихромной живописи, что известно каждому художнику. [155]

При подобного рода рассмотрении моя цель выходит за пределы создания более или менее точных правил. Для меня столь же важно вызвать дискуссию о теоретических методах. Методы анализа искусства до сих пор остаются довольно произвольными и нередко носят субъективный характер. Будущее потребует более точного и объективного пути, благодаря которому будет возможна коллективная работа в области науки об искусстве. Склонности и способности остаются здесь, как и везде, различными: каждый может выполнить лишь ту работу, которая ему по силам, поэтому особое значение будет придаваться более важным направлениям этой работы.

Тут и там возникала идея планомерно работающих институтов искусств, идея, которая, возможно, скоро будет воплощена в разных странах. Без преувеличения можно утверждать, что наука об искусстве, поставленная на широкую основу, должна иметь интернациональный характер: это интересно, но, разумеется, недостаточно – создать лишь европейскую теорию искусства. В этом отношении важны не столько географические или другие внешние условия (во всяком случае не только они одни), сколько различия во внутреннем содержании нации и, в первую очередь, в области искусства. Убедительный пример тому – черный траур у нас и белый траур у китайцев [156].

Большей противоположности в ощущении цвета быть не может – мы употребляем «черное и белое» так же часто, как обозначение «земля и небо». На этом основании мы все же можем определить глубинное и не сразу узнаваемое родство обоих цветов – оба являются молчанием, причем на нашем примере особенно остро выступает различие внутреннего содержания между китайцами и европейцами. Мы, христиане, после тысячелетий христианства воспринимаем смерть как окончательное молчание или, по моему определению, как «бесконечную дыру», а китайцы, язычники, истолковывают молчание как преддверие нового языка или, по моему определению, как «рождение» [157].

«Национальное» – это вопрос, который сегодня или недооценивается, или рассматривается лишь с внешней, поверхностно-научной точки зрения, поэтому его негативные стороны сильно выступают на передний план и полностью закрывают все другие. А эта другая сторона как раз и является внутренне главной. С этой последней точки зрения, сумма наций образовала бы не диссонанс, а созвучие. Возможно, в этом, к сожалению, кажущемся безнадежным случае искусство – на этот раз научным путем – неосознанно или непроизвольно действовало бы гармонизирующе. Введением к этому и могло стать осуществление идеи организации международных институтов искусств.

IB 2. Простейшие формы ломаной линии могут быть осложнены вследствие того, что к двум первоначальным образующим их линиям присоединятся несколько других. В этом случае точка получает не два, а несколько ударов, которые ради простоты производятся не многими, а лишь двумя чередующимися силами. Схематически тип этих многоугольных линий создается многими отрезками одинаковой длины, расположенными друг к другу под прямым углом. Исходя из этого, в двух направлениях модифицируется и бесчисленный ряд многоугольных линий:

1. благодаря комбинациям острого, прямого, тупого и свободного углов, и

2. благодаря звеньям различной длины.

Таким образом, многоугольные линии могут состоять из множества различных частей – от простейших до все более сложных.

Сумма тупых углов, которые имеют равные звенья, сумма тупых углов, имеющих неравные звенья, сумма тупых углов, сливающихся с острыми углами и имеющих равные или неравные звенья, сумма тупых углов, сливающихся с прямыми и острыми и т. д. (рис. 33).

Рис. 33. Свободная многоугольная линия

Эти линии называют также зигзагообразными , а при равных долях они образуют движущуюся прямую. Так, при острой форме они указывают высоту и, таким образом, вертикаль, а при тупоугольной форме имеют склонность к горизонтали, но при подобном образовании всегда сохраняют бесконечную возможность движения прямой.

Если, особенно при образовании тупого угла, сила последовательно прибывает, а угол увеличивается, то такая форма получает стремление к плоскости, и, в первую очередь, к кругу. Родство тупоугольных линий, кривых и круга не только является при этом внешним, но обусловлено и внутренней природой: пассивность тупого угла, его покорное отношение к окружению приводят его к величайшим углублениям, находящим завершение в наивысшем самоуглублении круга.

II. Если две силы одновременно оказывают свое воздействие на точку, и притом так, что сила одной и той же массы непрерывно и постоянно превосходит в давлении другую, то тогда возникает кривая линия в своем основном виде

1. простейшей кривой.

Она собственно является прямой, которая благодаря постоянному давлению со стороны сбилась со своего пути – чем больше было это давление, тем дальше шло отклонение от прямой и тем сильнее стал процесс напряжения вовне и, в конце концов, стремление к самозавершению.