Василий Кандинский - О духовном в искусстве. Ступени. Текст художника. Точка и линия на плоскости

б) с прямым углом – 90°4

в) с тупым углом – 135°.

IB 1. Ломаные линии простейших форм состоят из двух частей и являются результатом действия двух сил, которые прекращают это действие после одного-единственного толчка. Этот простой процесс ведет к важному отличию прямых линий от ломаных: ломаные в гораздо большей степени соприкасаются с плоскостью, они сами уже несут в себе нечто плоскостное. Плоскость находится в состоянии возникновения, ломаные линии же становятся мостом к этому. Различие между бесчисленными ломаными зависит исключительно от величины углов. На этом основании они могут быть схематически представлены в трех видах:

Остальные являются нетипичными острыми или тупыми углами, в разной степени отклоненными от этих типичных углов. Так, к трем первым ломаным линиям можно присоединить четвертую – несхематическую ломаную линию:

г) со свободным углом.

Исходя из этого эту ломаную линию надо назвать свободной ломаной линией.

Прямой угол одинок в своей величине и меняет лишь свое направление. Может быть только 4 прямых соприкасающихся угла – они либо соприкасаются вершинами, образуя крест, либо через соприкосновение расходящихся сторон создают прямоугольные плоскости – как правило, квадраты.

Горизонтально-вертикальный крест состоит из холода и тепла – это не что иное как центральное местоположение горизонтальных и вертикальных линий. Отсюда в зависимости от направления происходит холодно-теплая или тепло-холодная температура прямых углов, о чем подробнее будет говориться в главе «Основная плоскость».

Еще одно различие между простыми ломаными линиями зависит от степени длины отдельных ломаных частей – обстоятельство, меняющее основной звук этих форм.

Абсолютный звук данных форм зависит от трех условий и меняется следующим образом:

1. звук прямых с учетом уже упоминавшихся изменений (рис. 25)

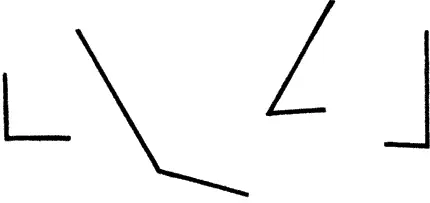
Рис. 25. Некоторые угловые линии

2. звук тяготения к более или менее острому напряжению (рис. 26)

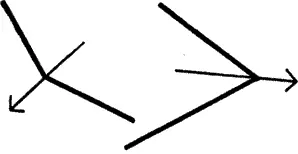
Рис. 26

3. звук тяготения к большему или меньшему завоеванию плоскости (рис. 27).

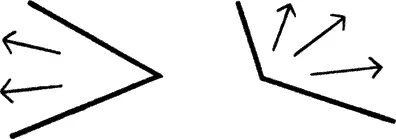
Рис. 27

Эти три звука могут образовать чистое трезвучие . Они также могут быть использованы как поодиночке, так и в паре, что зависит от общей конструкции: невозможно полностью разъединить все три звука, но при этом каждый из них до такой степени может заглушать остальные, что их будет едва слышно.

Самый объективный из трех типичных углов – прямой, он является самым холодным и делит квадратную плоскость на 4 части без остатка.

Самый напряженный и самый теплый – острый угол. Он разделяет плоскость на 8 частей без остатка.

Расширение прямого угла ведет к ослаблению направленного вперед напряжения, в связи с чем стремление к завоеванию плоскости соответственно усиливается. Этой жадности препятствует то, что тупой угол не в состоянии разделить всю плоскость без остатка: он вписывается в нее только два раза и оставляет часть в 90° незахваченной.

Тем самым три различных звука соответствуют трем этим формам:

1. холодность и господство,

2. острота и наивысшая активность, и

3. беспомощность, слабость и пассивность.

Три этих звука и, следовательно, угла дают замечательную графическую метафору художественного творчества:

1. острота и наивысшая активность внутреннего замысла (видение),

2. сдержанность и владение мастерством исполнения (осуществление),

3. чувство неудовлетворенности и ощущение собственного бессилия после окончания работы (названное среди художников «похмельем»).

Выше уже говорилось о 4 прямых углах, образующих квадрат. Взаимосвязи с живописными элементами здесь могут быть разобраны лишь кратко, но тем не менее можно провести параллель между ломаными линиями и цветами. Холодная теплота квадрата и его очевидная плоскостная природа указывают на красный цвет , который представляет переходную ступень между желтым и синим и несет в себе холодно-теплые свойства [152]. Не случайно так часто в последнее время встречается красный квадрат. Итак, параллель между красным цветом и прямым углом небезосновательна.

В ломаных линиях вида d нужно обратить внимание на специальный угол, расположенный между прямым и острым, – угол в 60° (прямой угол –30 и острый +15). Если два таких угла соединить друг с другом открытыми сторонами, то получится равносторонний треугольник с тремя острыми активными углами, которые указывают на желтый цвет [153]. Так, острый угол внутренне окрашен в желтый цвет .

Тупой угол проигрывает в степени агрессивности, остроты и теплоты, что несколько роднит его с безугольной линией, которая, как показано ниже, образует третью первичную схематическую плоскостную форму – крут. Пассивность же тупого угла , почти отсутствующее напряжение вперед придает ему легкую синюю окраску.

На этом основании могут быть пояснены дальнейшие взаимосвязи: чем острее угол, тем больше он приближается к острому теплу, и наоборот, тепло убывает по мере приближения его к прямому красному углу, он все более отклоняется к холоду до тех пор, пока не образует тупой угол (150°), типично синий угол, который является предчувствием кривой. Конечная цель этого процесса – образование круга.

Этот процесс может быть выражен графически:

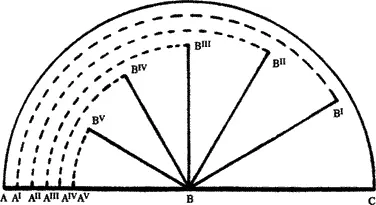
Рис. 28. Система типичных углов цветов

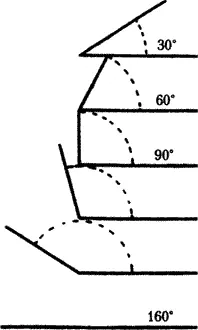
Рис. 29. Величина углов

Получается:

Следующий скачок в 30° осуществляет переход ломаных линий в прямые:

Так как типичные углы в своем дальнейшем развитии могут принять вид плоскости, то последующие отношения между линией, плоскостью и цветом становятся совершенно очевидными. Схематическое пояснение линейно-плоскостно-цветовых взаимосвязей может быть изображено таким образом: