Василий Кандинский - О духовном в искусстве. Ступени. Текст художника. Точка и линия на плоскости

Ацентральное построение в данном случае служило намерению усилить драматическое звучание.

Если, например, в только что приведенных примерах прямые линии заменить на простые кривые, то сумма звуков увеличилась бы втрое, поскольку каждая простая кривая линия состоит, как уже говорилось в главе «Линия», из двух напряжений, в результате которых появляется третье. Если впоследствии на смену простой кривой пришла бы волнообразная линия, то каждая волна представляла бы простую кривую с ее тремя напряжениями, и в соответствии с этим сумма напряжений продолжала бы увеличиваться. К тому же отношения каждой волны к границам ОП усложнили бы эту сумму более громкими или более тихими звуками [190].

Поведение плоскостей по отношению к ОП является темой для другого разговора. Но приведенные здесь закономерности и правила в полной мере распространяются и на эту специальную тему, давая направление, в котором она должна разрабатываться.

До настоящего момента здесь рассматривалась лишь квадратная ОП. Последующие прямоугольные формы – это результат преобладания или преимущества горизонтальной или вертикальной пограничных пар. В первом случае будет преобладать холодный покой, во втором – теплый, что, разумеется, и определяет с самого начала основной звук ОП. Устремленное вверх и вытянутое в длину – антиподы. Объективность квадрата исчезает, ее заменяет одностороннее напряжение ОП в целом, которое так или иначе будет влиять на все элементы ОП.

Надо еще отметить, что эти оба вида имеют более сложную природу, чем квадрат. В горизонтальном формате, к примеру, верхняя граница длиннее, чем боковые границы, и, таким образом, для элементов создается больше возможности для «свободы», что, впрочем, скоро вновь заглушается сокращением длины сторон. В вертикальном формате все происходит наоборот. Можно сказать, что границы в подобных случаях гораздо больше зависимы друг от друга, чем в квадрате. Это создает впечатление, будто бы здесь подыгрывает само окружение ОП, оказывая давление снаружи. Так, в вертикальном формате облегчается движение вверх, поскольку в этом направлении давление окружения снаружи почти совсем отсутствует и концентрируется главным образом на сторонах.

Последующие вариации ОП осуществляются благодаря применению разных комбинаций тупых и острых углов. Новые варианты возникают в случае, когда ОП образуется таким образом, что, например, она противостоит элементам правого верхнего угла как ведущая или вновь как препятствующая (рис. 99).

Наряду с этим существуют и многоугольные плоскости, которые в конце концов должны быть подчинены одной основной форме и поэтому являются лишь более сложными случаями данной основной формы, что не требует дальнейшего обсуждения (рис. 100).

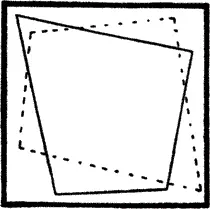
Рис. 99. Стимулирующая и сдерживающая (обозначена пунктиром) ОП

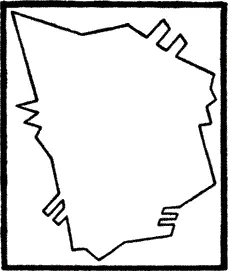
Рис. 100. Сложная многоугольная ОП

Величина углов может все больше и больше увеличиваться, а углы – становиться все более тупыми, до тех пор пока они в конце концов полностью не исчезнут и плоскость не станет кругом.

Это очень простой и одновременно очень сложный случай, который я уже подробно обсуждал. Здесь же лишь надо отметить, что как простота, так и сложность проистекают из-за отсутствия угла. Круг прост, так как давление его границ по сравнению с прямоугольными формами уравнено – различия не столь существенны. Он сложен, поскольку верх незаметно перетекает налево и направо, а левое и правое – вниз. Лишь четыре точки сохраняют звук четырех сторон квадрата, что соответствует и нашему эмоциональному восприятию.

Эти точки – 1, 2, 3, 4 – так же противостоят друг другу, как в четырехугольных формах: 1–4 и 2–3 (рис. 101).

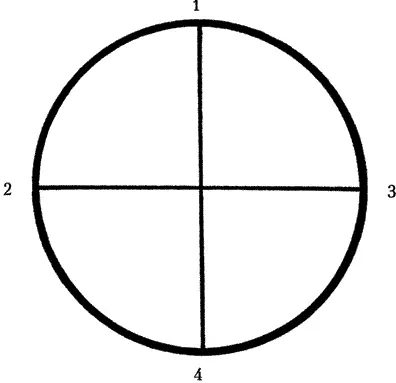
Рис. 101

Отрезок 1–2 – это постепенно прогрессирующее ограничение максимальной свободы по направлению сверху влево, которое на протяжении отрезка 2–4 переходит к твердости и т. д., до полного завершения круга. Уже описанное состояние напряженности четырех отрезков круга так же действует, как напряжения сторон квадрата. Таким образом, круг в основе содержит то же самое напряжение, что и квадрат.

Три основные плоскости – треугольник, квадрат, круг – это естественные производные планомерно движущейся точки. Если через центр круга провести две диагонали, которые своими вершинами будут связаны с горизонтальными и вертикальными линиями, то возникнет, по утверждению A. C. Пушкина, основа арабских и римских цифр (рис. 102).

Итак, здесь встречаются:

1. корни двух систем чисел, и

2. корни первичных форм искусства.

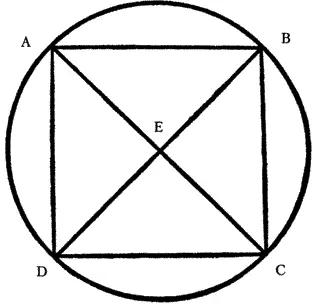
Рис. 102. Треугольник и квадрат, вписанные в круг, как первоисточник арабских и римских чисел (A. C. Пушкин. Сочинения, Петербург, издательство Анненкова, 1855, T. V. С. 16)

Если действительно существует подобное, из глубины идущее родство, то тем самым мы получаем определенное подтверждение нашему предчувствию одного и того же корня явлений, которые внешне выглядят абсолютно различными и полностью друг от друга отъединенными. Сегодня особенно важно отыскать эти общие корни. Такая необходимость не рождается на свет без внутреннего на то основания, но требуется много настойчивых попыток, чтобы наконец удовлетворить эту потребность. Эти необходимости имеют интуитивную природу. Поэтому интуитивно выбирается и путь к их удовлетворению. Для дальнейшего развития предполагается гармоничное соединение интуиции и расчета – одного из двух уже будет недостаточно.

Через равномерно сплющенный круг, в результате которого получается овал, мы идем дальше к свободным основным плоскостям, не имеющим углов и выходящим за пределы геометрических форм таким же образом, как это происходило и в случаях с угловыми формами. Основные принципы здесь остаются без изменений и будут различимы даже в самых сложных формах.

Все, что в общих чертах было сказано об основной плоскости, должно быть воспринято в качестве исходной схемы, в качестве подхода к пониманию смысла внутренних напряжений, имеющих внешнее воздействие.