Анатолий Фоменко - Как было на самом деле. Каждая история желает быть рассказанной

• 199 Носовский Г. В., Фоменко А. Т. «Статистические исследования событийных и биографических параллелей на материале английской хронологии и истории». – Семиотика и информатика. М., ВИНИТИ. Вып.34, 1994, с. 205–233.

• 200 Fomenko A. T. «Empirico-Statistical Analysis of Narrative Material and its Applications to Historical Dating». Volume 1: «The Development of the Statistical Tools». Volume 2: «The Analysis of Ancient and Medieval Records». (Монография). – Kluwer Academic Publishers. 1994. The Netherlands.

СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)

1994 год, 2 ноября. «Эврика» – Новая ежедневная газета, номер 18(24). Большая статья Георгия Танина «Точка отсчета» об А. Фоменко. О математике и живописи. Анонс: «Как знать, может быть, графике Анатолия Фоменко суждено стать точкой отсчета, которая будет вдохновлять мыслителей следующего тысячелетия?». 1994 год. Прекрасный альбом-календарь под названием «Картины художника А. Т. Фоменко», большого формата и великолепного качества, издан московским банком «Новый Символ». Это издание появилось благодаря инициативе председателя этого банка Сергея Александровича Черноморова, рис. 3.137. Это – яркий человек, выпускник физического факультета МГУ. Сейчас он – известный банкир. С. А. Черноморов давно интересовался моей графикой и живописью. Нас связывают многолетние дружеские отношения. Были опубликованы 12 факсимиле моих цветных и черно-белых работ. Издание широко распространялось, причем бесплатно, среди деловых и банковских кругов России и, в частности, служило яркой рекламой банку. Затем, на протяжении нескольких лет банк переиздавал этот альбом-календарь, каждый раз обновляя его за счет других моих графических и живописных работ. С. А. Черноморов – человек кипучей энергии, самых широких интересов, в частности, знаток философии и литературы. 1994 год. Публикации о наших исследованиях по новой хронологии. См. «Отклики на новую хронологию», книга «Реконструкция».

Рис. 3.137. С. А. Черноморов и А. Т. Фоменко.

Поездка на Международный Конгресс по динамическим системам в Уругвай, г. Монтевидео, с 27 марта по 1 апреля. Поехал вместе с моим талантливым учеником А. В. Болсиновым. Сделали там научные доклады по созданной мною и развитой потом вместе с моими учениками теории топологической классификации интегрируемых динамических систем.

Совместно с А. В. Болсиновым, рис. 3.138, мы обнаружили важный и неожиданный факт. Мы доказали, что знаменитая задача Якоби топологически траекторно эквивалентна не менее знаменитому интегрируемому случаю Эйлера в динамике твердого тела. Вкратце поясню суть дела. Что такое задача Якоби? Рассмотрим обычный трехосный эллипсоид в трехмерном пространстве, рис. 3.139, и геодезические на нем, то есть кратчайшие линии, реализующие минимум расстояния между любыми своими достаточно близкими точками. Характер поведения этих траекторий на эллипсоиде достаточно сложен. Их исследование и называется задачей Якоби. Выражаясь языком симплектической геометрии, можно сказать, что изучаются свойства геодезического потока на четырехмерном кокасательном пучке двумерной сферы, снабженной римановой метрикой эллипсоида. Эта задача важна для многих приложений.

Рис. 3.138. А. В. Болсинов и А. Т. Фоменко. Германия, Бонн, 19 августа 1998 года.

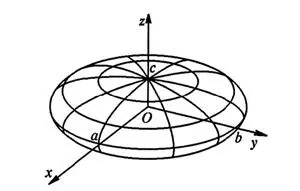
Рис. 3.139. Трехосный эллипсоид.

А что такое задача Эйлера? Рассмотрим динамику тяжелого твердого тела, закрепленного в его центре масс. Тогда движение тела описывается так называемыми дифференциальными уравнениями Эйлера. Важными частными случаями этой задачи являются, например, описание поведения корабля в океане, свободного полета самолета, то есть с выключенными двигателями и т. п., рис. 3.140, рис. 3.141.

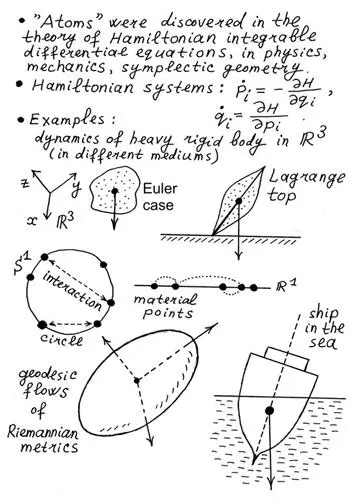
Рис. 3.140. Фрагмент тезисов моего доклада на международной топологической конференции в Греции 2010 года, где говорится о доказанной нами траекторной эквивалентности задач Эйлера и Якоби.

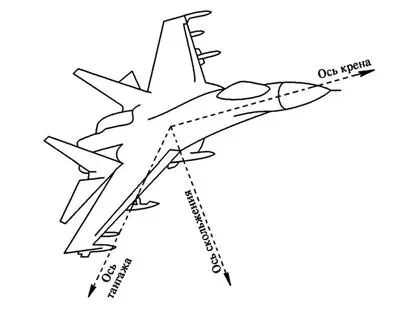
Рис. 3.141.Свободный полет самолета хорошо описывается уравнениями Эйлера. Случай Эйлера – это движение твердого тела, закрепленного в центре масс.

С точки зрения симплектической геометрии эта система уравнений Эйлера является динамической системой на том же четырехмерном фазовом пространстве, являющемся кокасательным пучком двумерной сферы. Таким образом, на одном и том же 4-мерном многообразии есть две замечательные системы уравнений, каждая из которых описывает свою «задачу». Обе эти задачи на первый взгляд кажутся совершенно различными и на протяжении многих лет, начиная с XIX века, изучались самостоятельно, без всякой связи одна с другой. И вот, совершенно неожиданно, применяя созданную мной теорию топологической классификации интегрируемых систем, мы обнаружили, что эти две динамические системы непрерывно траекторно эквивалентны.

Иными словами, имеется гомеоморфизм указанного четырехмерного пространства на себя, переводящий интегральные траектории одной системы в интегральные траектории другой системы. При этом параметр-время движения вдоль траекторий сохраняться не обязан.

Более того, мы показали, опираясь на важные результаты А. В. Болсинова, что с гладкой точки зрения эти системы траекторно не эквивалентны! То есть существует гомеоморфизм, переводящий интегральные траектории задачи Якоби в интегральные траектории случая Эйлера, но нет диффеоморфизма. Тем самым обнаружилось чрезвычайно тонкое различие между топологическими и гладкими свойствами этой известной системы.

В целом, получился яркий и глубокий результат. Между прочим, В. И. Арнольд был задет и раздражен, когда я сообщил ему эту нашу теорему и предложил ему наш подробный доклад на эту тему на его семинаре на мехмате. Однако Арнольд с ходу отказался нас выслушать, заявив, что хотя результат действительно яркий, но он считает, что «этот факт должен быть доказан по-другому, без использования теории Фоменко классификации интегрируемых систем». Я удивился такой форме отказа. Кстати, насколько мне известно, другого доказательства этого нашего результата до сих пор нет.

Тот факт, что в двойственном отношении Арнольда ко мне большую роль играла именно ревность, отмечали некоторые математики, близко знавшие Арнольда. В частности, как мне потом объяснили мои старшие коллеги по Академии (в частности, С. М. Никольский), именно из-за этой ревности Арнольд неожиданно выступил против меня на собрании Отделения во время выборов в академики, хотя буквально за день до этого, во время обсуждения кандидатур, сам же признавал, в присутствии свидетелей, что работы Фоменко – очень хорошие, и четко говорил, что собирается голосовать за меня. Но за одну ночь переменил мнение на противоположное. Наверное, поддался эмоциям.