Н. Белов - Алексей Васильевич Шубников (1887—1970)

Опыты по кристаллизационному давлению позволили рассмотреть механизм захвата частиц макроскопических размеров и распространить его на-захват примесей.

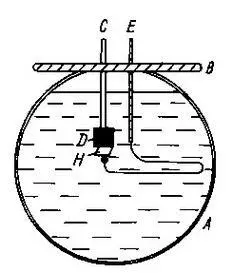
Рис. 7. Аппарат для измерения кристаллизационной силы.

А — сферический стеклянный сосуд; В — пластинка из зеркального стекла с двумя отверстиями; С — стеклянная палочка; D — каучуковая пробка; Е — стеклянная палочка, оттянутая в тонкую нить с шариком диаметром 2r; Н — кристалл, предназначенный для опыта.

С влиянием примесей на кинетику кристаллизации связаны многие явления, в том числе и образование вицинальных граней. А. В. Шубников показал, что угол между вициналями алюмокалиевых квасцов есть характерная константа кристаллов, выросших при определенном пересыщении :[87]. На рис. 8 представлена зависимость угла между вицинальными гранями октаэдра от пересыщения. Видно, что этот угол представляет собой непрерывную функцию от пересыщения. При отсутствии пересыщения он равен нулю. Отсюда следует важный вывод, что кристалл, выращенный бесконечно медленно, вицинальных граней не имеет. Можно думать, что такая зависимость определяется примесями в кристалле, содержание которых при малых скоростях, роста мало.

По вопросу о возникновении вицинальных граней существуют и другие гипотезы [46], например гипотеза о рациональности вициналей,. предложенная Шустером. Эта гипотеза не позволяет предсказать появление вициналей в зависимости от условий роста. Гипотеза Е. С. Федорова базируется на существовании в растворе двумерных пленок, образующих вицинальные грани. Эта гипотеза, однако, не дает ответа на вопрос о том, почему в случае алюмокалиевых квасцов вицинальные грани образуются только на грани октаэдра. Гипотеза «скучивания» М. В. Ерофеева и А. Н. Карножицкого предполагает двойниковое срастание и прорастание нескольких кристаллов под очень малыми углами друг к другу. Однако в этом случае кристалл должен состоять из участков, отличающихся друг от друга углами поворота. Гипотеза непараллельного расположения молекул в узлах кристаллической решетки также не в состоянии объяснить, почему такая непараллельность характерна только для' грани октаэдра. И, наконец, существует гипотеза Эренфеста, которая основана на том, что капиллярные постоянные вицинальных граней близки к граням простого символа. А. В. Шубников отдавал-предпочтение гипотезам Шустера и Эренфеста, которые позволяли объяснить причину возникновения вициналей на транш октаэдра и отсутствия их на грани куба.

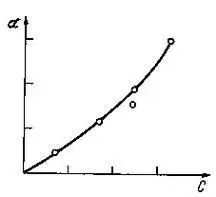
Рис. 8. Зависимость угла между вицинальными гранями и степенью пересыщения раствора.

Примеси и механические частицы оказывают существенное влияние не только на процесс роста, но и на процесс зарождения кристаллов. Об этом свидетельствуют данные, полученные А. В. Шубниковым совместно с В. Ф. Парвовым при кристаллизации хлористого аммония из раствора под действием электрического поля [257]. При этом интенсивно возникают новые центры кристаллизации. Было замечено, однако, что во влажной атмосфере этот эффект исчезает. Причина явления, видимо, заключается в том, что под действием электрического поля из атмосферы в раствор попадают возбуждающие кристаллизацию твердые частицы хлористого аммония. Если атмосфера влажная, то адсорбция влаги на частицах хлористого аммония приводит к их растворению.

Сила, действующая на частицу, f = qE (здесь q — заряд частицы; Е — напряженность поля в точке, где находится частица) направлена вдоль соответствующей силовой линии в сторону возрастания напряженности. Эта сила возникает из-за неодинакового распределения индуцированных зарядов на противоположных сторонах частицы.

Форма роста кристаллов является основным морфологическим признаком, позволяющим установить условия их образования [225]. Нормальная скорость роста из расплава грани может быть представлена в виде:

V i= a i(Т i-Т k),

где Ti — температура равновесия между средой и гранью i-й простой формы; Т k— температура среды у поверхности кристалла; a i— постоянная.

Если для исследуемого кристалла все величины a i, T iизвестны, то по ним может быть построена зависимость скорости роста от температуры Т kи воспроизведена форма кристалла для любой температуры Т k.

Предположим, что теплообмен между кристаллом и средой осуществляется путем молекулярной теплопроводности и тетрагональный кристалл имеет только грани призмы {100} и базиса {001}. Если скорость роста граней базиса v 1больше скорости роста граней призмы v 2, то кристалл будет иметь столбчатый габитус. При обратном соотношении скоростей — пластинчатый.

Также предположим, что v 1>v 2, тогда прямая v 1= а 1(Т 1—Т k) лежит выше кривой v 2= а 2(Т 2—Т k), как показано на рис. 9.

Если кристалл возник при значительном переохлаждении расплава (T k

x/z = v 1/v 2,

где х — ширина кристалла по оси Х; z — его высота по оси Z ┴(001).

Вследствие выделения скрытой теплоты температура кристалла повысится до Т" k. При Т" k, близкой к Т 2, отношение v 1/v 2может стать очень большим, при Т k= Т 2 -бесконечно большим. Это значит, что в подобных условиях рост граней призмы может прекратиться полностью, вследствие чего кристалл будет приобретать все более удлиненную форму. При обратном соотношении v 12он примет уплощенную форму. Такие формы в термодинамическом отношении менее выгодны, чем форма сферолита, образующегося в результате расщепления столбчатого кристалла вдоль оси Z и пластинчатого кристалла вдоль плоскости базиса.

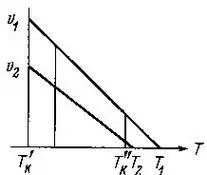
Рис. 9. Зависимость нормальных скоростей v 1и v 2граней базиса и призмы тетрагонального столбчатого кристалла от температуры Т.

Форма шара, покрытого маленькими гранями, имеющими наименьшее из возможных значений удельной поверхности энергии, в энергетическом отношении является более выгодной, чем многогранная. Расщепление сферолита происходит по плоскости спайности, а образован он плоскостями, обладающими наибольшей удельной поверхностной энергией.

Для сферолита, сплошь покрытого гранями {001}, при равенстве объемов кристалла V kи сферолита V sимеют место следующие соотношения:

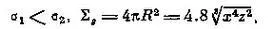
где Σ g— поверхность сферолита; R — его радиус.