Михаил Колесников - Лобачевский

А в эвклидовом мире дела шли своим обычным, лишенным логики порядком. По иронии судьбы Магницкого записали в декабристы! Дескать, выступал против Николая! Шишков передал-таки все доносы Михаила Леонтьевича новому монарху. Рассвирепевший Николай приказал начать расследование по делу «бывшего попечителя Казанского учебного округа». К Магницкому приставили жандарма. Следствие вели генерал-лейтенант Желтухин и бывший ректор университета, некогда изгнанный Магницким, а ныне казанский губернский прокурор Гавриил Ильич Солнцев. Магницкий уже заранее был обречен. Особенно после того, как следователи обнаружили хищения больших казенных сумм…

Второе событие — доклад Николая Ивановича Лобачевского на заседании физико-математического факультета Казанского университета 11 (по новому стилю 23) февраля 1826 года — осталось почти незамеченным.

Этот день ознаменовал начало новой эры в развитии мировой геометрической мысли, он стал днем рождения неэвклидовой геометрии.

Присутствовавшие на заседании профессора слушали докладчика невнимательно. Их больше занимала история падения Магницкого. Каждый дрожал за свое местечко, с тревогой ожидал вызова к грозному Желтухину и язвительному Солнцеву. Даже Никольский чувствовал себя причастным к декабрьскому восстанию и побаивался ареста, ссылки. Много курили. Всем казалось странным, нелепым, что в такое зыбкое, суматошное время можно еще заниматься какими-то постулатами и теоремами, создавать новую геометрию, когда и старая-то может не пригодиться.

— За прегрешения наши… — бормотал Никольский и опасливо косился на Николая Ивановича.

В облике Лобачевского ему сейчас чудилось нечто сатанинское. Вот Николай Иванович остановился у доски, какая-то чужая, нездешняя улыбка пробрела по его губам. Свел острые изогнутые брови, надвинул шапку темно-русых волос почти на глаза, наклонил голову. Стоит, заслонив спиной чертеж, и, окидывая всех угрюмо-задумчивым взглядом, говорит:

— …Главное заключение, к которому пришел я с предположением зависимости линий от углов, допускает существование геометрии более в обширном смысле, нежели как ее представил нам первый Эвклид. В этом пространном виде дал я науке название Воображаемой Геометрии, где как частный случай входит употребительная геометрия с тем ограничением в общем положении, какого требуют измерения в самом деле…

В чем же сущность, сокровенный смысл открытой Лобачевским неэвклидовой геометрии?

Почему великий геометр назвал ее Воображаемой?

Почему эвклидова геометрия является частным — вернее, предельным — случаем геометрии Лобачевского?

Реальна ли геометрия Лобачевского в смысле соответствия физическому пространству, существует ли поверхность, на которой справедлива новая геометрия, или же она бесполезный плод фантазии, досужий вымысел, игра воображения, формальное доказательство независимости пятого постулата от других эвклидовых аксиом? Какая из двух геометрий с большей точностью описывает реальный мир?

Шаг за шагом мы проследили, как Лобачевский подходил к открытию новой геометрии, проследили в той мере, в какой возможно рассказать о сокровенной, тончайшей работе гениального ума, где из хаоса мимолетных наблюдений на основе опыта и интуиции рождается небывалая истина, постепенно выкристаллизовывающаяся в виде четкой формулы.

Первое значительное открытие Лобачевского состояло в доказательстве независимости пятого постулата геометрии Эвклида от других положений этой геометрии.

Вторым открытием была уже сама логически непротиворечивая система новой геометрии. На свою геометрию он смотрел именно как на теорию, а не как на гипотезу.

Придя к логическому заключению, что в мировом пространстве, а возможно и в микрокосме, сумма углов треугольника должна быть меньше двух прямых, Лобачевский смело выдвинул свою исходную аксиому, свой постулат и построил необычную геометрию, так же, как и эвклидова, лишенную внутренних противоречий. Воображаемой назвал не потому, что считал ее формальным построением, а потому, что она пока оставалась доступной лишь воображению, а не опыту. Его не покидала мысль вновь вернуться к измерению космических треугольников и установить истину.

Ничего не меняя в «абсолютной» геометрии, он лишь заменил пятый постулат антипостулатом, антиэвклидовой аксиомой: через указанную точку можно провести множество прямых, не пересекающих данную.

На чертеже это выглядит так:

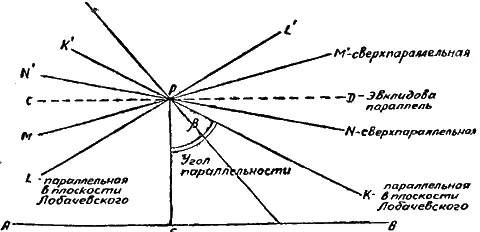
Лобачевский изменил само понимание параллельных линий. У Эвклида непересекающиеся и параллельные — одно и то же, у Лобачевского: из всех, не пересекающих данную прямую АВ (см. чертеж), лишь две прямые называются параллельными — это K 1РK и LPL 1 . Все остальные, находящиеся в пучке между параллельными, таковыми не считаются (в современной литературе их называют сверхпараллельными).

Поэтому постулат уточняется: если дана прямая АВ и не лежащая на ней точка Р, то через точку Р в плоскости АВР можно провести две прямые, параллельные данной прямой АВ.

Параллельными Лобачевский, следовательно, называет такие, которые отделяют непересекающие от пересекающих данную прямую АВ.

Расстояние между прямой АВ и каждой из параллельных не остается постоянным — уменьшается в сторону параллелизма и увеличивается в противоположную сторону. Параллельные прямые могут близко подойти друг к другу, но они не могут пересечься.

Плоскость, в которой существуют такие параллельные, принято называть плоскостью Лобачевского. Эта плоскость вовсе не «плоская» в эвклидовом смысле.

В эвклидовой плоскости угол параллельности неизменен и всегда равен 90°; в геометрии Лобачевского он может принимать все значения — от 0 до 90°. Следовательно, эвклидова геометрия есть частный (предельный) случай геометрии Лобачевского, в которой угол параллельности переменный.

Геометрически величина угла параллельности зависит от длины X перпендикуляра РЕ; то есть если перпендикуляр уменьшается, угол параллельности увеличивается, постепенно приближаясь к 90°.

Весьма условно на чертеже это можно было бы представить так:

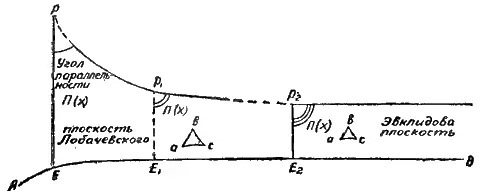
Другими словами: когда точка Р стремится к совпадению с точкой Е, то есть когда X стремится к нулю, тогда угол параллельности стремится к 90°.

Таким образом, в новой геометрии существует взаимозависимость угла и отрезка. Когда угол параллельности прямой, то есть равен 90°, взаимозависимость исчезает. В эвклидовой геометрии ее нет. В неэвклидовой она представляет наиболее значительный момент.