Игорь Дмитриев - Упрямый Галилей

И наконец, еще об одном важном допущении, сделанном Декартом, необходимо упомянуть. Обсуждая столкновение мяча с твердой и гладкой плоской поверхностью, он полагает:

…Стремление к движению по некоторому направлению, подобно самому движению и, вообще говоря, любой другой величине, может быть разбито на все составляющие, какие только можно вообразить; нетрудно представить себе, что скорость мяча, летящего из A в B [рис. 3.8], делится на две составляющие, одна из которых заставляет его спускаться с линии AF к линии CE , а другая одновременно вынуждает мяч переместиться от левой стороны AC к правой FE таким образом, что обе они (то есть обе указанные составляющие. – И.Д .), соединенные вместе, направляют мяч в B по прямой линии AB . Далее легко понять, что встреча мяча с поверхностью земли может изменить лишь одну из этих скоростей (то есть только одну из компонент скорости. – И.Д .), но никак не другую; так как встреча должна помешать скорости, заставляющей мяч спускаться с AF к CE вследствие того, что земля занимает все пространство, находящееся под CE , то как же она могла бы препятствовать другой скорости (то есть горизонтальной компоненте скорости. – И.Д .), побуждающей мяч перемещаться вправо, ведь она никоим образом не противостоит ему в этом направлении? 1689

По сути, Декарт говорит здесь о двух допущениях. Первое сводится к тому, что при ударе мяча о землю изменяется только вертикальная компонента его скорости. Второе допущение более существенно: когда Декарт говорит, что «стремление к движению по некоторому направлению, подобно самому движению <���…> может быть разбито на <���…> составляющие», он имеет в виду мысль, сформулированную им в предыдущей главе «La Dioptrique»: «легко поверить, что действие или стремление к движению, о которых я сказал, что их следует принимать за свет, должны следовать тем же законам, что и движение» 1690. «Нет, месье Декарт, – мог бы возразить внимательный читатель, – не легко и очень даже не легко поверить, что нечто (как вы там его ни называйте – действием или стремлением к движению), способное распространяться с бесконечной и только с бесконечной скоростью, что утверждалось всего абзацем выше, вдруг, как выясняется, следует законам движения с конечными скоростями и, как выяснится в следующей главе, может менять свою скорость». Но в тексте «La Dioptrique», как и в переписке Декарта, нет ничего, что могло бы рассеять сомнения и сделать картезианскую мысль «ясной и отчетливой». Поэтому читателю остается только продолжить знакомство с «La Dioptrique».

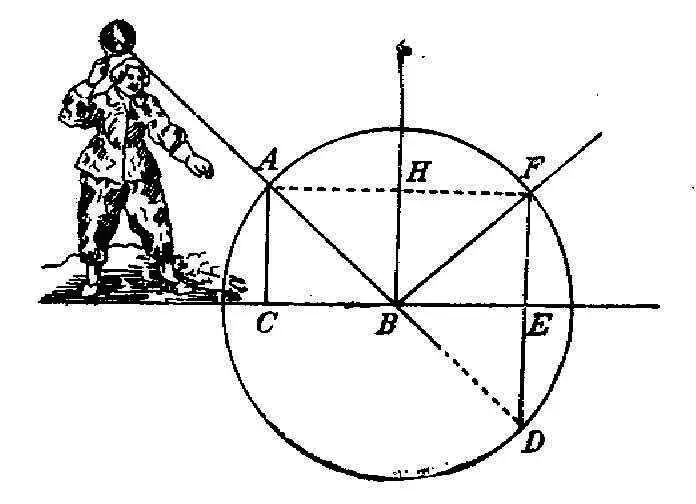
Рис. 3.8. К рассмотрению Декартом столкновения мяча с твердой и гладкой плоской поверхностью

Обращаясь к явлению преломления света, Декарт вносит в принятую им ранее аналогию с теннисным мячом новые нюансы.

Прежде всего предположим, – пишет он, – что мяч, выброшенный из A [рис. 3.9] по направлению в B , встречает в точке B не поверхность земли, а кусок материи CBE , которая настолько слаба и редка, что он может прорвать ее и пройти насквозь, теряя только часть скорости, например, половину. Если это так, то для того, чтобы знать, каким путем мяч должен следовать, примем опять во внимание, что его движение совершенно отличается от стремления к движению скорее в одну сторону, чем в другую, откуда вытекает, что их значение должно рассматриваться отдельно; учтем также, что из двух составляющих этого стремления лишь та из них, которая вынуждает мяч спуститься сверху вниз, может быть сколько-нибудь изменена при встрече с материей <���…>. Далее, описав из центра B окружность AFD и начертив под прямыми углами к CBE три прямых линии AC , HB , FE таким образом, чтобы расстояние между FE и HB было в два раза больше, чем между HB и AC , мы увидим, что мяч должен стремиться к точке I ; поскольку мяч, проходя через кусок материи CBE , теряет половину своей скорости, постольку он должен употребить, чтобы опуститься вниз от точки B до какой-нибудь точки окружности AFD , в два раза больше времени, чем то, которое ему понадобилось для прохождения от A к B ; а так как мяч ничего не теряет из своего стремления продвигаться к правой стороне, то за удвоенное время [по сравнению с тем, которое ему потребовалось, чтобы переместиться от линии AC до линии HB ] он должен проделать в эту сторону путь в два раза больший и, следовательно, достичь некоторой точки прямой FE в то же самое мгновение, когда он приближается к какой-либо точке окружности AFD ; это возможно только при условии, если мяч направляется к точке I , ибо она является единственной под куском полотна CBE , где окружность AFD и прямая линия FE пересекаются 1691.

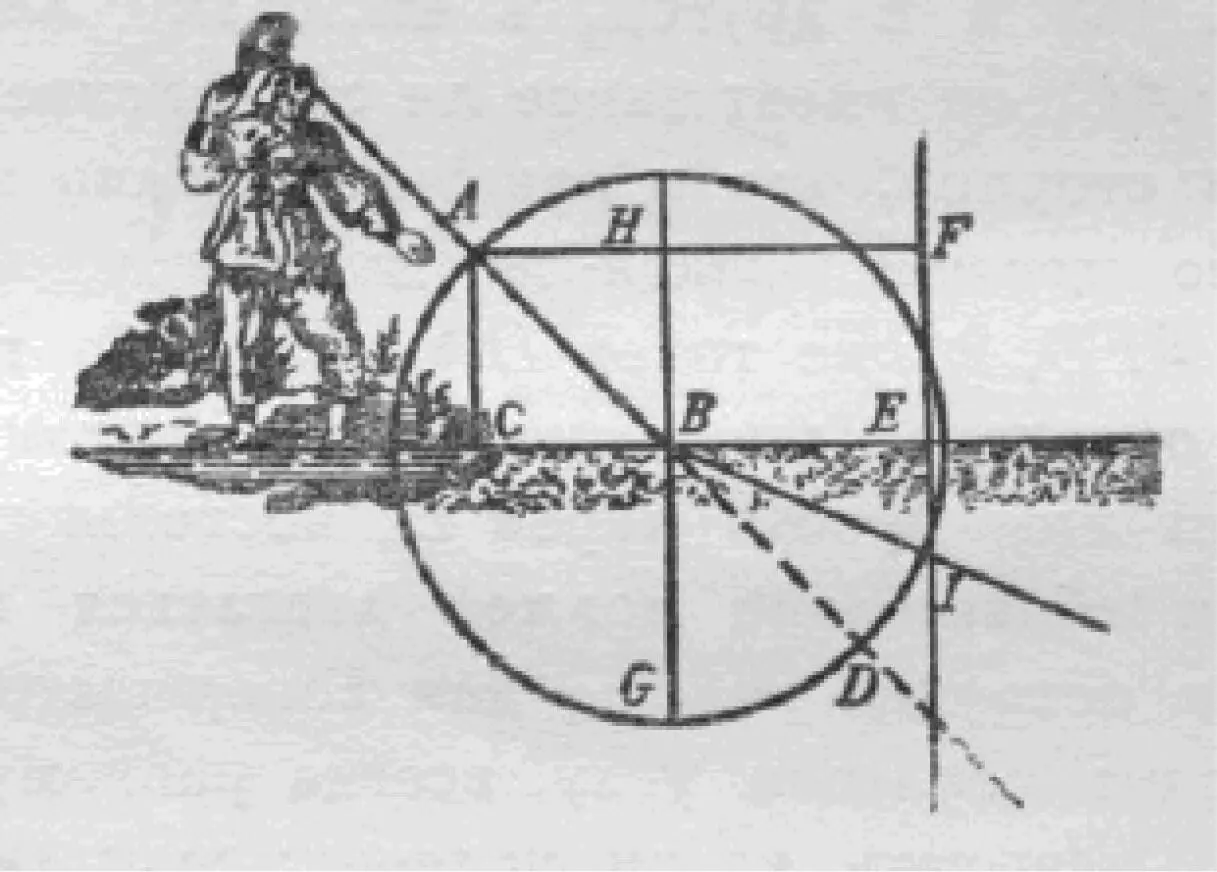
Рис. 3.9. К рассмотрению Декартом столкновения мяча с куском материи

Теперь, предлагает Декарт, заменим кусок полотна поверхностью воды, которая «отнимет у мяча» тоже половину скорости (как и в предыдущем случае). Все приведенные рассуждения при этом останутся в силе и «мяч неизбежно направится из точки B по прямой линии не к D , а к I » 1692[рис. 3.10]. Часть воды, «заполняющей все пространство от B до I, сопротивляется то больше, то меньше по сравнению с воздухом, наличие которого мы ранее предполагали; однако это не означает, что вода должна в большей или в меньшей степени отклонить мяч, ибо она легко раздается ( car il se peut ouvrir ), с одинаковой легкостью открывая ему путь как в одну сторону, так и в другую, по крайней мере, если, как и ранее, исходить из предположения, что ни тяжесть или легкость мяча, ни его величина или форма, ни какая-нибудь иная причина не меняют его направления» 1693.

Описав движения мяча в разных ситуациях, Декарт обращается в анализу движения света, который, переходя из воздуха в воду (то есть из менее плотной в более плотную среду), отклоняется, но, как показывают наблюдения, в направлении, противоположном отклонению мяча, в сторону отрезка HG [рис. 3.11]. Чтобы объяснить этот факт, Декарт допустил, что мяч, «брошенный из A в B , отбрасывается снова, находясь в точке B , поверхностью CBE , увеличивающей силу его движения, например, на одну треть, таким образом, чтобы он мог потом совершить за двойной промежуток времени такой же путь, какой он проделывал за тройной; подобное действие следует рассматривать так, как если бы мяч встречал в точке B тело такого характера, что он мог бы пройти через его поверхность CBE на одну треть легче, чем через воздух. Из приведенного доказательства ( sic! – И.Д .) с очевидностью вытекает, что если описать окружность AD [рис. 3.11], как было сделано ранее, и провести линии AC , HB и FE таким образом, чтобы между FE и HB было бы расстояние на треть меньшее, чем между HB и AC , то точка I , где прямая линия FE и окружность AD пересекаются, укажет место, к которому мяч, находясь в точке B , должен отклониться» 1694. Таким образом, расстояние BI определяется соотношением BE = GI = 2 BC /3, и перпендикуляр FE , будучи продолжен вниз до пересечения с окружностью, пересечет ее в точке I . В итоге Декарт делает следующий вывод: «поскольку мяч, идущий по прямой линии из A в B , отклоняется в точке B и отсюда направляется к точке I , постольку это означает, что сила, или легкость, с какой он входит в тело CBEI , относится к той, с которой он покидает тело ACBE , как расстояние, отделяющее AC от HB , относится к расстоянию между HB и FI , то есть как отрезок CB относится к отрезку ВE » 1695. Последнее утверждение эквивалентно так называемому закону синусов 1696, или, другое название, закон Снелия 1697. Действительно, если угол ABH – это угол падения ( i ), а угол IBG – угол преломления ( r ), то поскольку sin i = AH / AB , sin r = GI / BI и AB = BI = 1, то sin i = AH = CB и sin r = GI = BE . Следовательно, CB / BE = sin i / sin r .