Светлана Ржевская - Управление качеством. Практикум

В одном стандарте не допускается применение разных систем обозначения единиц величин.

Обозначения единиц величин могут быть применены в заголовках (подзаголовках) граф и строк таблиц и пояснениях символов, используемых в формулах, а в остальных случаях, например в тексте стандарта, – только при числовых значениях этих величин.

Пример – 10 кг.

7.2 В пределах одного стандарта для одного и того же показателя (параметра, размера) применяют, как правило, одну и ту же единицу величины. Например, длину трубы указывают по всему тексту стандарта в метрах, толщину стенки трубы – в миллиметрах, а электрическое напряжение – в вольтах.

7.3 Если в тексте стандарта приведен ряд числовых значений величины, которая выражена одной и той же единицей величины, то обозначение единицы величин указывают только после последнего числового значения.

Пример – 1,0; 1,5; 2,0; 2,5 мм.

7.4 Интервалы чисел в тексте стандарта записывают со словами «от», «до» (имея в виду: «от . до . включительно»), если после чисел указана единица величины, или через тире, если эти числа являются безразмерными коэффициентами.

Если в тексте стандарта приводят диапазон числовых значений величины, то обозначение единицы этой величины указывают за последним числовым значением диапазона, за исключением знаков «%», «°C», «…°».

Примеры

1… от 10 до 100 кг;

2 … от 65% до 70%;

3 … от 10 °C до 20 °C.

Если интервал чисел охватывает порядковые номера, то для записи интервала используют тире.

Пример – … рисунки 1—14.

7.5 Недопустимо отделять единицу величины от числового значения (разносить их на разные строки или страницы), кроме единиц величин, приводимых в таблицах.

Формулы и уравнения

1 Общие требования к изложению формул и уравнений в нормативно–технической документации

Не допускается одной буквой (греческой, латинской, готической и др.) обозначать разные физические или математические объекты.

Математические выражения, не представляющие собой уравнения или формулы, могут быть написаны в строке основного текста, например: "При F 3 /F 4 > 20 процесс происходит с повышением температуры ."

Несколько небольших формул, располагаемых в красную строку, допускается помещать в один ряд (а не одну под другой).

Номер для многострочной формулы ставится против последней ее строки.

В тексте ссылку на порядковый номер формулы следует начинать со слов «формула», «уравнение», «выражение», и затем в круглых скобках указывают номер формулы, например: "В формуле (4.15) приведены … ".

Если ссылка на порядковый номер формулы находится внутри выражения, заключенного в круглые скобки, то их следует заменить на прямые скобки, например: «Удельная теплоемкость кислорода [см. уравнение (43)] увеличивается с ростом температуры».

В формулах следует применять в первую очередь круглые скобки ( ), во вторую – прямые [ ], в третью – фигурные { }, в четвертую – угловые скобки < >.

Двоеточие ставят перед формулами только тогда, когда этого требует построение текста, предшествующего формуле.

После формул ставится тот знак препинания, который необходим исходя из построения фразы:

– если формулой заканчивается фраза – точка;

– если заканчивается главное предложение – запятая (например, перед словом «где», начинающим экспликацию).

Указанные знаки препинания следует помещать непосредственно за формулами до их номера.

Между идущими подряд формулами ставят точку с запятой.

Коэффициенты в формулах следует писать впереди буквенных выражений слитно с ними.

Точку на средней линии как знак умножения не ставят:

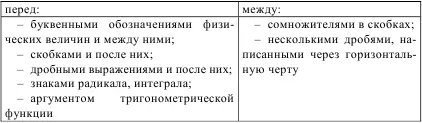
Знак умножения следует применять между числовыми сомножителями (13·5; 7·1432) или когда вслед за аргументом тригонометрической функции стоит буквенное обозначение, а также для отделения сомножителей от выражений, относящихся к знакам логарифма, интеграла, радикала и т.п.

Основным знаком умножения является точка на средней линии (·). Знак умножения в виде косого креста (×)применяется чаще всего для размеров, между числовыми сомножителями в формулах, при переносе формулы с одной строки на другую на знаке умножения, для векторного произведения векторов.

Знак корня √(радикал) следует писать так, чтобы его горизонтальная черта полностью накрывала все подкоренное выражение.

Многоточие (отточие) внутри формулы применяется в виде трех точек на нижней линии строки. Запятые (при перечислении величин), а также знаки сложения, вычитания и равенства ставят перед отточием и после него, например:

f(x 1, x 2, x 3, … , x n).

Обозначение единицы физической величины в математическую формулу следует помещать только после подстановки числовых значений величин и затем после промежуточных и конечных результатов вычисления, например:

В экспликацию – расшифровку приведенных в формуле буквенных обозначений величин – следует, как правило, включать все обозначения, помещенные как в левой, так и в правой части формулы. Если перед формулой помещено обозначение единицы, приводимое в левой части формулы, то в экспликации ее можно не приводить.

Последовательность расшифровки буквенных обозначений величин должна соответствовать последовательности расположения этих обозначений в формуле. Если правая часть формулы представляет собой дробь, то вначале поясняются обозначения величин, помещенных в числителе, а затем – в знаменателе.

После формулы перед экспликацией следует поставить запятую, затем с новой строки набрать от левого края слово «где» (без двоеточия после него), за ним – обозначение первой величины и его расшифровку, выравнивая колонку расшифровки по знаку «тире» (эти знаки должны образовать вертикаль).

Если расшифровка обозначения не помещается в одной строке, то вторая и следующая строки расшифровки должны начинаться от левого края первого слова расшифровки первой строки. В конце каждой расшифровки рекомендуется ставить точку с запятой, а в конце последней расшифровки – точку.

Обозначения единиц физических величин в каждой расшифровке следует отделять запятой от текста расшифровки.

При повторении в последующих формулах обозначений величин, приведенных в предыдущих формулах, допускается повторение их расшифровки, если формулы отделены друг от друга. Можно ограничиться ссылкой на порядковый номер формулы, при которой приведена расшифровка.