Азамат Киреев - Наибольший общий делитель (НОД)

В данной книге приводятся четыре алгоритма нахождения наибольшего общего делителя, необходимая теория, формулы, 29 примеров с решениями, 140 упражнений с ответами.

В таблице приведем два способа определения НОД.

Не является рациональным способом нахождения наибольшего общего делителя двух чисел

Выпишем все делители чисел 32 и 24.

Делители числа 32: 1, 2, 4, 8, 16, 32.

Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.

Общими делителями 24 и 32 являются: 1, 2, 4, 8.

Наибольший из них – 8. Обозначается НОД(24;32)=8.

Замечание.Вышеизложенный алгоритм №0 не является рациональным способом нахождения НОД (им можно воспользоваться в том случае если вы забыли способы нахождения НОД).

Определение 3.Натуральные числа a и b называют взаимно простыми, если их наибольший общий делитель равен 1, то есть НОД( a ; b ) = 1.

Иначе выражаясь, если числа a и b не имеют никаких общих делителей, кроме 1, то они взаимно просты.

Пример 3.

1) Числа 2 и 5 взаимно простые (и сами они простые);

2) 2 и 9 взаимно простые (2 – простое, 9 – составное);

3) 8 и 9 взаимно простые (и оба они составные);

Замечание.Как видно из случаев, приведенных в примере 2, понятия «простые числа» и «взаимно простые числа» не имеют особой связи между собой.

Правило.Если одно из данных чисел [36] является делителем другого числа [72], то оно [36] будет являться наибольшим общим делителем данных чисел [72 и 36].

Для вычисления по алгоритму №1 необходимо знать формулы

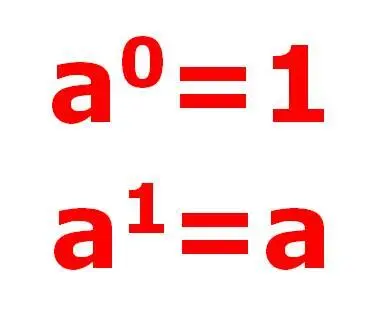
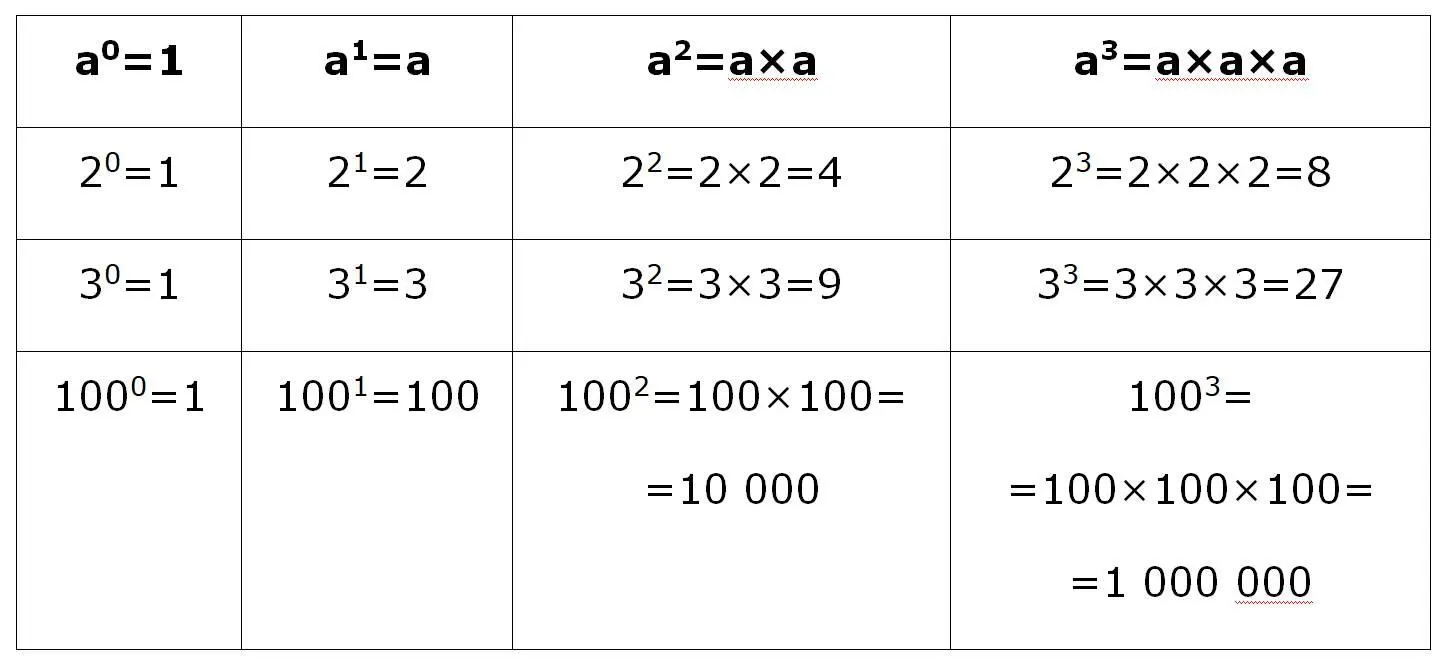
Замечание.Формулу a 0=1 мы будем использовать «справа налево», то есть 1=a 0

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.