Юрий Казаринов - Успешный менеджер: кейс-стади по принятию решений. Учебно-методическое пособие

● Y 2l– испытание водой;

● Y 22– испытание нефтью.

Вариант Y 23– испытание воздухом – неприемлем вследствие того, что недостаточное проходное давление не обеспечивает возможность создания необходимой степени сжатия.

Измерение предпочтений решений по достижению целей проводилось в шкале порядка методом ранжирования. Ранжирование проведено отдельно для случаев проектного и проходного давлений. Результаты решений представлены в табл. 2.

На первом этапе решения задачи целесообразно для каждого уровня давления выбрать наиболее предпочтительный вид носителя. Поэтому необходимо свернуть ранжировки (по уровням давления) в условиях достижения всех целей и с учетом их весов. Для «осторожной» стратегии ЛПР свертка ранжировок проводится по методу медианы [24].

Свертка ранжировок альтернативных решений при проектном давлении методом медианы включает процедуры:

1. Построение матриц парных сравнений по каждой цели, элементы которых определяются по правилу:

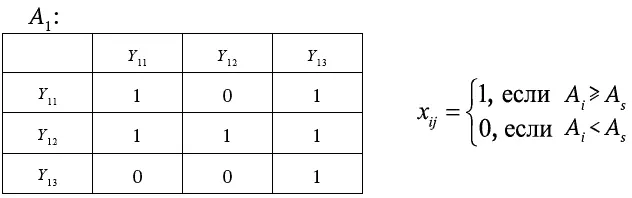
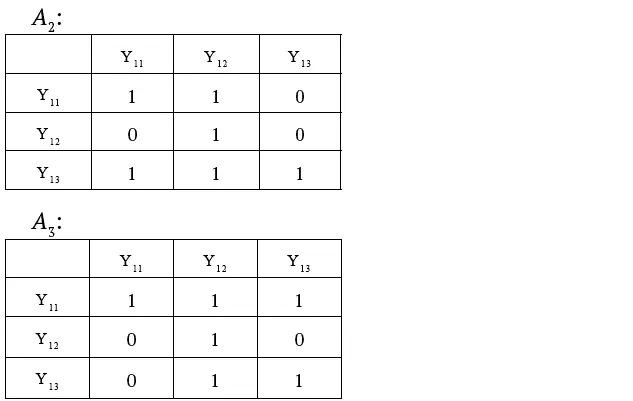
2. Построение промежуточной матрицы, каждый элемент которой является суммой элементов предыдущих матриц по каждой цели, умноженных на соответствующие коэффициенты важности этих целей:

3. Построение обобщенной матрицы, каждый элемент которой определяется по правилу:

4. Построение обобщенной ранжировки: Y 13> Y 11> Y 12. Свертка ранжировок при проходном давлении методом медианы проводится аналогично и имеет вид: Y 22> Y 21(табл. 2).

Таблица 2

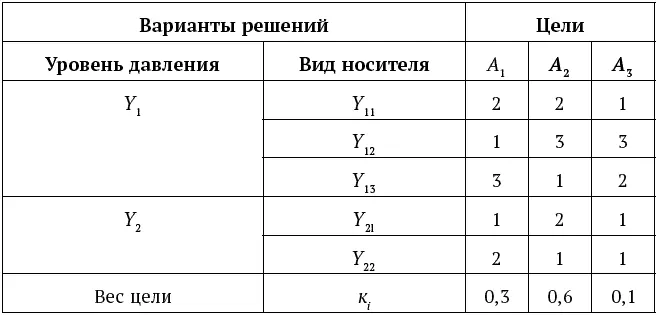
Обобщенная ранжировка решений при проектном давлении: Y 13> Y 11> Y 12 [25], где символ «>» означает предпочтение, доминирование одного объекта (варианта решения) над другим.

Обобщенная ранжировка решений при проходном давлении: Y 22> Y 21. Следовательно, нефтепровод нужно испытывать нефтью либо при проходном, либо при проектном давлении.

На втором этапе решения задачи необходимо определить наиболее предпочтительный уровень давления нефти в магистрали, исходя из ранжировок ЛПР решений на множестве целей (табл. 3).

Таблица 3

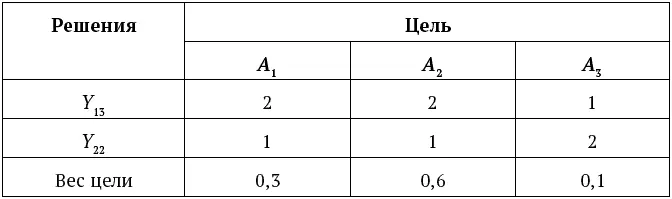
Свертка ранжировок решений Y 13 и Y 22 по всем целям как методом медианы, так и суммы рангов приводит к одному упорядочению решений Y 22 >Y 13. Выбор оптимального решения, проведенный вышеуказанными методами, показал, что таким решением является решение Y 22 – проведение испытания нефтью при проходном давлении. Это решение было реализовано на практике и оказалось эффективным. Следует отметить, что, несмотря на кажущуюся простоту выполнения ранжировки решений, такое качественное измерение требует большой компетентности ЛПР в области проведения испытаний и, кроме того, точного учета конкретных условий и обстоятельств, сопровождающих проведение испытаний

Цель планирования выполнения программы – это распределение мероприятий, детализация мероприятий на работы, упорядочение работ во времени, оценка интенсивности потребления ресурсов.

Планирование включает следующие стадии: 1) построение сетевой модели выполнения работ; 2) составление календарного плана.

Процедуры построения сетевой модели включают:

● составление сетевого графика;

● оценку времени выполнения работ;

● оценку ресурсов на выполнение работ;

● расчет временных, ресурсных и вероятностных характеристик сетевого графика в целом;

● корректировку сетевого графика и его характеристик для обеспечения выполнения программы в директивный срок с заданной вероятностью.

Процедуры построения календарного плана: 1) определение начала и конца работ; 2) оценка интенсивности потребления ресурсов.

Сетевая модель работ по выполнению программы является инструментом для планирования выполнения работ во времени и оценки вероятностей выполнения работ в директивный срок. Одновременно сетевая модель является инструментом оперативного управления, позволяющим корректировать ход выполнения работ.

Сетевая модель [26](сетевой график, сеть) отражает комплекс работ (операций) и событий, связанных с реализацией некоторого решения, в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет более четко выявить взаимосвязи этапов реализации решения и определить оптимальный порядок выполнения этих этапов для сокращения сроков выполнения всего комплекса работ.

Математический аппарат сетевых моделей базируется на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества связей, соединяющих вершины, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т. е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае – неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для двух любых его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В менеджменте чаще всего используются два вида графов: дерево и сеть.

Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида «сеть».

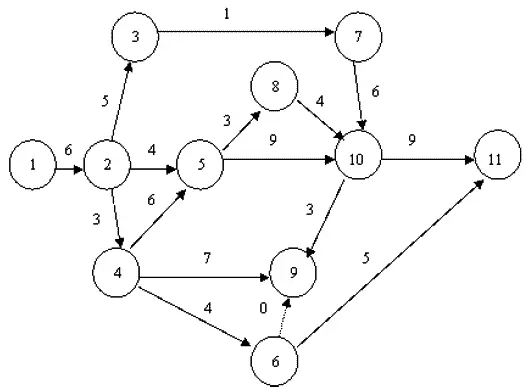
Рис. 2. Сетевая модель, состоящая из 11 событий и 16 работ, продолжительность выполнения которых указана над работами [27].