Андрей Юревич - Социальная психология знания

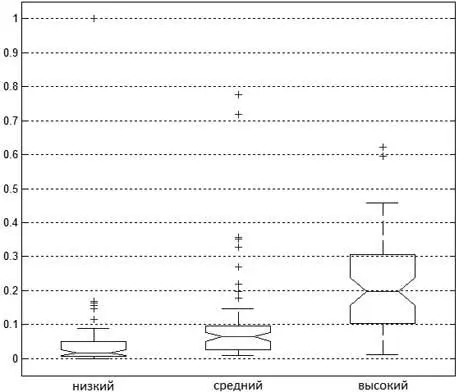
Рис. 3. Box plot для значений D iпри соответствующем уровне фактора I i, полученных из (Lynn, Vanhanen, 2002)

На основе анализа рисунка 3 можно сделать выводы:

1. С ростом значения I i растет медиана значений D i.

2. С ростом значения I i увеличиваются как значения квантилей q 1, q 3 , 9-й и 91-й процентили, так и расстояние между ними, т. е. увеличивается разброс значений D i.

3. Распределение значений D i в выборке становится более симметричным относительно своей медианы с ростом I i.

Приведем результаты аналогичных процедур обработки для данных, полученных в имитационной модели (таблица 2, рисунок 4).

Таблица 2 [7] Столбцы в таблице 2 аналогичны столбцам в таблице 1.

Так же, как и в случае данных из (Lynn, Vanhanen, 2002), вероятность необоснованного отклонения гипотезы Н 0 весьма мала, ≈7,59.10 –10(см. таблицу 2). Следовательно, так же как и в предыдущем случае, с большой степенью уверенности (1 – p ≈ 1) можно утверждать, что значения параметра D i, полученные с помощью имитационной модели, зависят от значений параметра I i. Оценим характер этого влияния, используя график box plot для данных имитационной модели (см. рисунок 4).

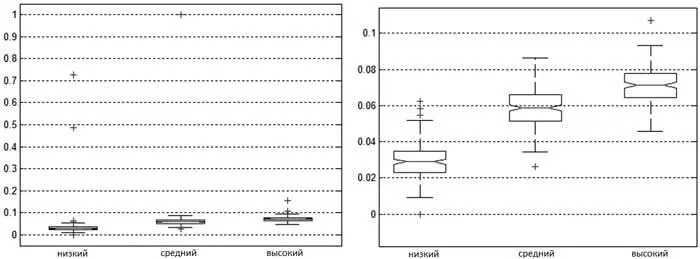
Рис. 4. Box plot для значений D iпри соответствующем уровне фактора I i, полученных из имитационной модели (справа – увеличение картинки «ящика с усами» для уровня фактора I i«низкий» и «средний»)

Как видно из рисунка 4, трем уровням фактора I i соответствуют следующие значения медианы D i: «низкий» – 0,03, «средний» – 0,59, «высокий» – 0,73.

На основе рисунка 4 можно сделать вывод: с ростом значения I i растет медиана значений D i.

Сравнивая выводы о характере зависимостей в данных (Lynn, Vanhanen, 2002) и данных, полученных из имитационной модели, мы можем отметить, что 1-й вывод для данных из книги (Lynn, Vanhanen, 2002) воспроизводится моделью. Эффекты 2 и 3 в списке выводов для реальных данных не воспроизводятся имитационной моделью. Возможной причиной этого является отсутствие фактического общего рынка, который, в силу конкуренции между странами на рынке товаров, мог бы снизить ВВП некоторых стран с высокими значениями средних компетенций I i, тем самым способствуя эффектам 2 и 3 в списке эффектов для данных (Lynn, Vanhanen, 2002).

Анализ результатов имитационной модели

Как было показано в предыдущем разделе, ВВП страны тем выше, чем выше средний уровень компетенций работников в данной стране. Используя результат доказанной выше теоремы, построим с помощью имитационной модели зависимость максимально возможного ВВП max GDP i от среднего уровня компетенций I i в странах, а также рассчитаем и построим зависимость процента потерь ВВП rl i (максимально возможный ВВП при фиксированном распределении доходов минус реализовавшийся ВВП при том же распределении доходов) от среднего уровня компетенций I i:

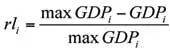
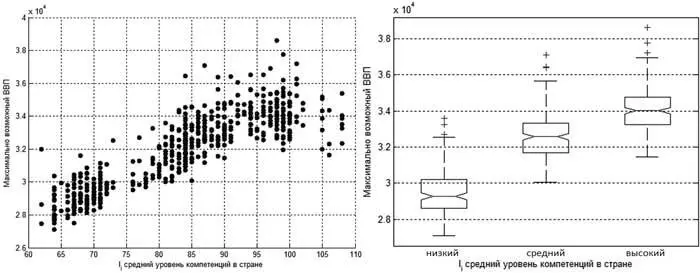
Рис. 5. Зависимость максимально возможного ВВП от среднего уровня компетентности в стране (слева иллюстрация данных, справа средние значения и статистические оценки по трем группам значений: «низкий», «средний» и «высокий» уровень I i)

Как видно из рисунка 5, зависимость max GDP i от среднего уровня компетенций I i имеет схожий с GDP i характер, однако процент потерь ВВП rl i примерно один и тот же для разных значений среднего уровня компетенций I i в стране (рисунок 6). Следовательно, характер зависимости GDP i от I i не определяется потерями от того, что распределение количества товара по группам качества по-разному сегментировано в группах стран с разными значениями среднего уровня компетенций I i.

На величину выражения (5), помимо степени сегментированности распределения количества товара по группам качества, определенного выше, очевидно влияет распределение доходов потребителей ( IC ). Сравним распределение доходов потребителей для различных групп значений средних компетенций I i.

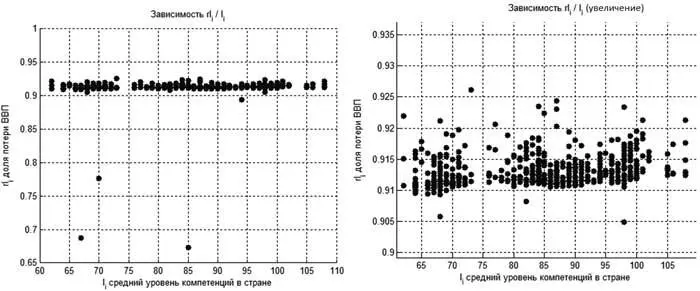
Рис. 6. Зависимость процента потерь ВВП от среднего уровня компетентности в стране (сверху иллюстрация данных, снизу средние значения и статистические оценки по трем группам значений: «низкий», «средний» и «высокий» уровень Ii)

Из рисунка 7 видно, что распределение доходов для стран с высокими значениями I i доминирует над распределением доходов стран с низкими значениями I i. Это и предопределяет для этих стран, согласно формуле (5), более высокие значения GDP i. Значения доходов работников из формулы (4) определяются распределением капитала бизнесменов в данной стране, и оно имеет схожий характер с распределением дохода работников (распределение капитала бизнесменов для стран с высокими значениями I i определяет распределение капитала стран с низкими значениями I i ). Для выяснения причин, лежащих в основе различия в распределении капитала бизнесменов между группой стран с низкими и высокими значениями I i, рассмотрим следующий пример расчетов. Внесем одно изменение в алгоритм имитационной модели: изменим правило назначения работников на подзадачи порогового типа. Для каждой страны с фиксированным средним уровнем компетенций I i заменим минимальный порог каждой пороговой подзадачи θ j в формуле (7) на величину θ j+ I i– const. Таким образом, подзадачи всех задач становятся одинаково доступны для индивидов из всех стран (т. е. мы расширяем потенциальное множество задач, доступных для выполнения в каждой стране, сделав его одним и тем же для разных значений I i ). Одновременно мы не изменили вклад в качество товара, определяемого частью открытых подзадач. Приведем зависимость ВВП от значений среднего уровня компетенций в странах I i (рисунок 8).

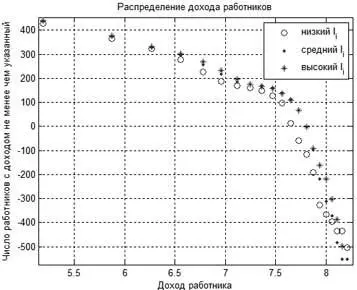
Рис. 7. Распределение дохода среди работников в странах с низким, средним и высоким уровнями средней компетенции в стране. График приведен в двойном логарифмическом масштабе (по обеим осям отложены логарифмы указанных величин)