Андрей Юревич - Социальная психология знания

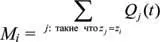
То есть имеется товара в количестве M 1 с уровнем качества z 1 ( t ) (самый качественный товар), товара в количестве M 2 с уровнем качества z 2 ( t ) и т. д., с убыванием значения z. Как следует из определения, M 1 + M 2 + … + M p равно общему количеству товара, произведенному в текущем такте .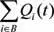

Пусть p ≥ s, тогда примем следующее определение.

Определение 3. Будем говорить, что распределение количества товара по группам качества сегментировано, если для соответствующего ему вектора ( M 1, M 2, …, M p ) и вектора распределения совокупного размера сбережений потребителей ( N 1, N 2 , …, N s ) выполнено условие:

M 1 = N 1, M 2 = N 2 , …, M s= N s.

Теорема. При фиксированном распределении совокупного размера сбережений потребителей N ( t ) значение GDP ( t ) в (5) достигает максимума тогда и только тогда, когда распределение количества товара по группам качества M ( t ) сегментировано.

Схема доказательства

Для удобства доказательства далее будем представлять сумму (5) как сумму ненулевых слагаемых, упорядоченных по убыванию, где каждое слагаемое соответствует цене IC, которую заплатил отдельный потребитель. Число слагаемых очевидно равно числу потребителей и фиксированно.

Необходимость. Предположим, что M ( t ) не сегментировано и GDP ( t ) достигает своего максимального значения. Тогда существует i, 1 ≤ i ≤ s такой, что M 1 = N 1, …, M i ≠ N i. Рассмотрим два случая:

M i< N i

В данном случае число слагаемых в (5) со значением IC i меньше, чем для случая сегментированного M ( t ) (если бы M i= N i ). В то же время число слагаемых со значениями IC > IC i такое же, а слагаемых со значениями IC < IC i больше – при одном и том же общем числе слагаемых. Следовательно, значение (5) в указанном случае меньше, чем в случае сегментированного M ( t ).

M i > N i

В данном случае слагаемые в (5) со значением IC i не встретятся, вместо этого будет большее число слагаемых с IC < IC i. При фиксированном числе слагаемых значение (5) меньше, чем в случае сегментированного M ( t ).

Достаточность. Пусть M ( t ) сегментировано. В соответствии с алгоритмом покупки товара и в силу сегментированности M ( t ), в сумме (5) будет N 1 слагаемых с максимальным возможным значением IC 1 (число таких слагаемых уже нельзя увеличить, а можно только уменьшить, уменьшив общую сумму), N 2 слагаемых со значением IC 2 (их число также нельзя увеличить) и т. д. до N s слагаемых с значением IC s. Таким образом, получается, что сумма (5) принимает максимально возможное для себя значение.

Результаты работы имитационной модели

Сравнение результатов модели и предметных данных

Для соотнесения результатов имитационной модели и данных по странам проведем нормировку показателей средней компетентности I i в стране i и ВВП на душу населения D i для результатов, полученных с помощью имитационной модели и данных из работы (Lynn, Vanhanen, 2002):

На рисунке 2 проиллюстрированы два набора данных после нормировки:

• данные по реальным странам (слева), полученные из (Lynn, Vanhanen, 2002);

• данные имитационной модели (справа), полученные в момент модельного времени t = 25, когда характер зависимости, изображенной на рисунке 2, не меняется в течение более 10 тактов. Ниже, при расчетах параметров модели, рассматриваются данные на этом такте времени.

Визуально на рисунке 2 мы можем отметить наличие роста мат. ожидания и дисперсии D i при росте значения I i. Оценим статистически степень влияния фактора I i на D i отдельно по данным для стран из (Lynn, Vanhanen, 2002) и отдельно по данным, полученным в имитационной модели.

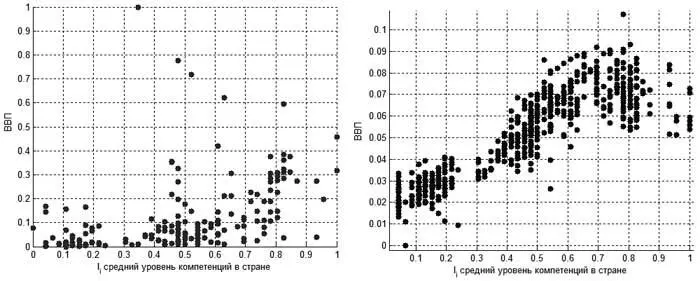
Рис. 2. Иллюстрация данных I iи D i, полученных из (Lynn, Vanhanen, 2002) (слева) и имитационной модели (справа)

Для оценки степени влияния I i на D i посредством однофакторного дисперсионного анализа проверим наличие статистической зависимости показателя D i от уровней фактора I i (групп различных значений) (Кобзарь, 2006). Разобьем значения I i на три равные непересекающиеся группы (три уровня фактора I i: «низкий», «средний» и «высокий»), сформируем три выборки значений D i для соответствующего уровня фактора I i. Рассчитаем уровень значимости p гипотезы Н 0:

« Все три выборки принадлежат одной генеральной совокупности или разным генеральным совокупностям с равными средними арифметическими» (если гипотеза H 0 неверна, то параметр I i оказывает существенное влияние на D i ).

Уровень значимости p есть вероятность необоснованно (ошибочно) отвергнуть (считать неверной) гипотезу H0 . Проведем расчеты отдельно для данных из работы Линна и для данных, полученных из имитационной модели.

Анализ данных из работы Линна показывает, что вероятность необоснованного отклонения нулевой гипотезы крайне мала: ≈9,44 .10 –9(см. таблицу 1). Следовательно с большой степенью уверенности (1 – p ≈ 1) можно утверждать, что значения параметра D i зависят от значений параметра I i на основе данных, собранных в (Lynn, Vanhanen, 2002).

Таблица 1 [5] В таблице 1, в столбце SS представлены результаты расчета: – внутригрупповой дисперсии (Columns), характеризующей изменение средних в каждой из трех групп различных значений параметра Ii; – межгрупповой дисперсии (Error), характеризующей рассеяние значений Di вне влияния фактора Ii; – общей выборочной дисперсии (Total). В столбце df приведено число степеней свободы по каждому виду дисперсии. В столбце MS – среднее значение суммы квадратов разностей по каждому виду дисперсии, определяемое как отношение SS/df. В столбце F – значение статистики Фишера для MS. Значение уровня значимости p(Prob > F) для рассчитанного значения статистики F приведено в последнем столбце.

Оценим характер влияния I i на D i. На рисунке 3 проиллюстрируем результат обработки данных из (Lynn, Vanhanen, 2002) в виде графика box plot («ящик с усами»). На этом рисунке вдоль оси Ох размещены три уровня фактора I i: «низкий», «средний» и «высокий» в соответствующем порядке. Для каждого из трех уровней фактора I i нарисован «ящик с усами» (фигура синего цвета – «ящик», пунктирные вертикальные прямые – «усы»). Горизонтальная линия («талия» у ящика) обозначает медиану выборки значений параметра D i, соответствующих уровню фактора I i («низкий», «средний» и «высокий»). Как видно из рисунка 3, уровням фактора I i соответствуют следующие значения медианы D i: «низкий» – 0,017, «средний» – 0,065, «высокий» – 0,2. Нижняя и верхняя границы каждого из ящиков иллюстрируют первую и третью квантили q 1 и q 3 для выборки D i соответственно [6] В промежутки значений [0, q 1 ] и [q 3 , 1] попадает по 25 % от общего числа точек D i из выборки. . Длина усов каждого из ящиков определяются значениями: нижняя – 9-й процентили, верхняя – 91-й процентили. Данные, выходящие за пределы усов (выбросы), отображаются на графике в виде крестиков.