БСЭ - Большая Советская энциклопедия (Пр)

В разностных формулах П. р. удаётся несколько раз использовать уже вычисленные значения правой части. Решение ищется в виде линейной комбинации у ( xi ), h iи разностей D ih j, где

h j= hf ( x j, y j ); Dh j= h j+1- h j;

D ih j= D i-1h j+1- D i-1h j.

Примером разностной формулы П. р. является экстраполяционная формула Адамса. Так, формула Адамса, учитывающая «разности» 3-го порядка:

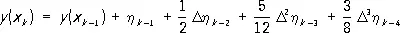
даёт решение у ( х ) в точке x kс точностью до величин порядка h 4 .

Для уравнений 2-го порядка можно получить формулы численного интегрирования путём двукратного применения

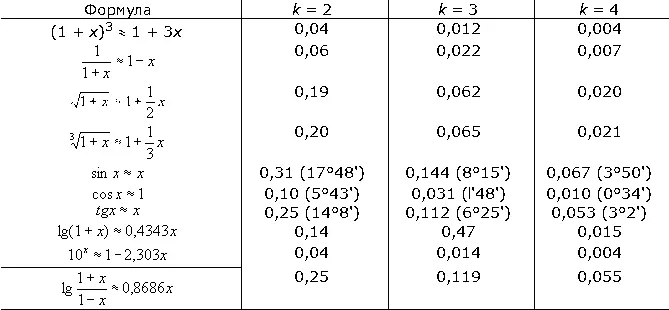
формулы Адамса. Норвежский математик К. Стёрмер получил формулу:

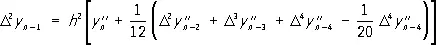
особенно удобную для решения уравнений вида у'' = f ( x, у ) . По этой формуле находят D 2 y n-1, а затем y n+1 = y n +D y n+ 1+ D 2 y n-1 . Найдя y n+1 , вычисляют y’’ n+1 = f ( x n+1, y n+1 ) , находят разности и повторяют процесс далее.

Указанные выше численные методы распространяются и на системы дифференциальных уравнений.

Значение численных методов решения дифференциальных уравнений особенно возросло с распространением ЭВМ.

Кроме аналитических и численных методов, для П. р. дифференциальных уравнений применяются графические методы. В простейшем из них строят поле направлений, определяемое дифференциальным уравнением, т. е. в некоторых точках рисуют направления касательной к интегральной кривой, проходящей через эту точку. Затем проводят кривую так, чтобы касательные к ней имели направления поля (см. Графические вычисления ).

Лит.: Березин И. С., Жидков Н. П., Методы вычислений, 2 изд., т. 2, М.. 1962; Бахвалов Н. С., Численные методы, М., 1973: Коллатц Л., Численные методы решения дифференциальных уравнений, пер. с нем., М., 1953; Милн В. Э., Численное решение дифференциальных уравнений, пер, с англ., М., 1955.

Приближённые вычисле'ния,вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. П. в. возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов П. в. принято называть численными методами .

Приближённые фо'рмулы,математические формулы, получаемые из формул вида f ( x ) = f* ( x ) + e( х ), где e( х ) рассматривается как погрешность и после оценки отбрасывается. Таким образом, П. ф. имеет вид f ( x ) » f* ( x ) .

Например, П. ф. (1 + х ) 2» 1 + 2 x получается из точной формулы для (1 + х ) 2при малых | x |; этой формулой можно пользоваться при вычислении с точностью до сотых, тысячных, десятитысячных, если | x | соответственно не больше 0,0707..., 0,0223..., 0,00707... Эта П. ф. даёт результат тем более точный, чем х ближе к 0. Но так бывает не всегда. Например, точность П. ф. tg 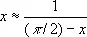тем больше, чем х ближе к p/2.

Выше (стр. 555) приведено несколько наиболее употребительных П. ф., причём показано, какого числа не должно превосходить | x | , чтобы формула давала k точных десятичных знаков.

Часто П. ф. получают с помощью разложения функций в ряды, например в ряд Тейлора. Чтобы уверенно применять П. ф., необходимо иметь оценку разности между точным и приближённым выражениями функции. Зная, например, что разность между sin x и двучленом 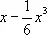не превосходит по абсолютному значению 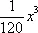, легко убедиться, что П. ф. 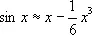даёт значения sin x с точностью до сотых, тысячных, десятитысячных, если х соответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°).

«Прибо'й», легальное большевистское издательство, создано в ноябре 1912 в Петербурге во время «страховой кампании» (1912—1914), с 1913 начало выпуск литературы по вопросам социального страхования рабочих; с июля 1913 стало издательством ЦК РСДРП, по указанию которого главное внимание уделяло изданию политической агитационно-пропагандистской литературы по вопросам рабочего движения. Вышли сборники: «Марксизм и ликвидаторство» со статьями В. И. Ленина, «Страхование рабочих в России и на Западе» (2-й и 3-й выпуски), календарь «Спутник рабочего на 1914» (со статьей Ленина «Стачки в России») и др. В работе издательства участвовали А. И. Ульянова-Елизарова, М. С. Ольминский, Ф. И. Драбкина и др. В начале 1-й мировой войны 1914—18 в связи с цензурными репрессиями «П.» прекратил свою деятельность; издательство возобновило работу в марте 1917. Были выпущены работы Ленина «Письма о тактике». Письмо 1-е с приложением Апрельских тезисов; «Задачи пролетариата в нашей революции»; «Уроки революции»; «Материалы по пересмотру партийной программы»; «Грозящая катастрофа и как с ней бороться». В 1918 влилось в книгоиздательство «Коммунист».

Лит.: Шварцман С. М., Книгоиздательство «Прибой» (1913—1914), в сборнике: «Книга», № 13, М., 1966.

Прибо'йв ткачестве, продвижение уточной нити вдоль основы к опушке (краю) ткани. Одна из основных операций при формировании ткани на ткацком станке . Наиболее распространённый рабочий орган для П. — бердо ; перемещающее уточную нить одновременно по всей ширине основы. П. на некоторых станках осуществляется непрерывно с помощью прижимов-уплотнителей утка ( круглоткацкий станок ) , профилированных дисков (многозевные ткацкие машины).

Прибо'й, явление разрушения морской (озёрной) волны, происходящее в результате разбивания волн непосредственно у берега, при этом колебательные движения воды сменяются возвратно-поступательным движением прибойного потока . П. — основной фактор разрушения абразионных берегов и образования пляжей, сопровождаемый перемещением наносов на пляжах на аккумулятивных берегах.