БСЭ - Большая Советская энциклопедия (Пр)

Лит.: Уолш Д.-Л., Интерполяция и аппроксимация рациональными функциями в комплексной области, пер. с англ., М,, 1961; Маркушевич А. И., Теория аналитических функций, т. 2, М., 1968; Смирнов В. И.. Лебедев Н. А., Конструктивная теория функций комплексного переменного, М. — Л., 1964; Мергелян С. Н., Приближения функций комплексного переменного. в кн.: Математика в СССР за сорок лет. 1917—1957, т. 1, М., 1959, с. 383-98; Гончар А. А., Мергелян С. Н., Теория приближений функций комплексного переменного, в кн.: История отечественной математики, т. 4, кн. 1, К,, 1970, с. 112—78.

А. А. Гончар.

Приближённое интегри'рованиеопределённых интегралов, раздел вычислительной математики, занимающийся разработкой и применением методов приближённого вычисления определённых интегралов .

Пусть y = f ( x ) — непрерывная функция на отрезке [ a, b ] и интеграл

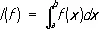
Если для функции f ( x ) известны значения первообразной F ( x ) при x = а и х = b, то по формуле Ньютона — Лейбница

I ( f ) = F ( b ) - F ( a )

В противном случае приходится искать др. пути вычисления l 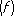. Одним из путей является построение квадратурных формул, приближённо выражающих значение I 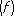в виде линейной функции некоторого числа значений функции f ( x ) и её производных. Квадратурной формулой, содержащей только значения функции f ( x ) , называют выражение вида

S n 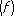= 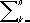A kf ( x k ) ,

в котором точки x k, k = 1, 2,..., n, x k Î [ a, b ] , называют узлами, а коэффициенты A k— весами.

Для каждой непрерывной функции f ( x ) значение I 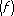может быть вычислено с помощью сумм S n 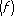с любой точностью. Выбор квадратурной формулы определяется классом W, к которому относят конкретную функцию f ( x ) , способом задания функции и имеющимися вычислительными средствами. Погрешностью квадратурной формулы называется разность

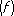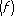R n = I - S n .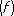

Квадратурная формула содержит 2 n + 1 не зависящих от функции f ( x ) параметров: n, x k, A k ( k = 1, 2,..., n ) , которые выбирают так, чтобы при f Î W погрешность её была допустимо малой. Точность квадратурной формулы для f Î W характеризует величина rn (W) — точная верхняя грань ½ Rn 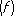½ на множестве W:

.

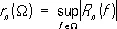Пусть

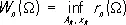
Квадратурная формула, для которой W n (W) = r n (W), называется оптимальной на классе П. Веса и узлы в оптимальной квадратурной формуле могут быть произвольными или подчинёнными определённым связям.

Различают два класса квадратурных формул: элементарные и составные. Разработано несколько методов построения элементарных квадратурных формул. Пусть w q ( x ) , q = 0, 1,..., — полная система функций в классе W, и любая f ( x ) Î Q достаточно хорошо приближается линейными комбинациями первых функций w q ( x ) . Пусть l (w q ) , q = 0, 1, 2,..., можно вычислить точно. Для каждого n параметры квадратурной формулы можно определить из требования, чтобы

I (w q ) = S n (w q ) , q = 0, 1,..., m,

для возможно большего значения m. В методе Ньютона — Котеса в квадратурной формуле выбираются узлы x k, а определению подлежат веса A k. В методе Чебышева на веса A k заранее накладываются некоторые связи [например, A k = ( b - а ) /n ] , а определению подлежат узлы x k. В методе Гаусса определяются и веса A k и узлы x k. В методе Маркова j узлов ( j < n ) считают заранее известными, а определяют веса и оставшиеся узлы. Точность полученных такими методами квадратурных формул существенно повышается при удачном выборе функций w q ( x ) .

Формулы Ньютона — Котеса строятся на основе системы функций w q = x q, q = 0 , 1,...; узлы x k разбивают отрезок интегрирования на равные части. Примерами таких формул являются прямоугольников формула , трапеций формула и Симпсона формула .

Поскольку заменой переменной интегрирование по [ а, b ] сводится к интегрированию по отрезку [-1, 1], то для определения весов и узлов элементарных формул на [ а, b ] достаточно знать их для отрезка [-1, 1]. В случае составных формул исходный интеграл представляется в виде:

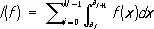
и для вычисления интегралов по отрезкам [ a i, a i+1 ] применяются элементарные квадратурные формулы.

В формулах Гаусса m = 2 n — 1, а при а = — 1, b = 1 узлы x k являются корнями Лежандра многочлена P n ( x ) степени n, а

A k= 2(1 - x 2 k ) -1( P’ n ( x k )) -2

Квадратурная формула Чебышева существует при A k = l/n, l = b - а и x k Î [ a, b ] лишь для n = 1,..., 7, 9; в ней m = n - 1. Применение равных весов минимизирует вероятностную ошибку, если значения f ( x ) содержат независимые случайные ошибки с одинаковой дисперсией.

При вычислении интегралов от функций с периодом l наиболее употребительны квадратурные формулы типа Гаусса:

.

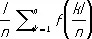Существуют квадратурные формулы для вычисления интегралов вида

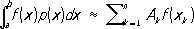
где р ( х ) — фиксированная, т. н. весовая функция. Её подбирают так, чтобы для всех f Î W функции f ( x ) хорошо приближалась линейными комбинациями функций w q ( x ) .

Для приближённого вычисления неопределённых интегралов их представляют как определённые интегралы с переменным верхним пределом и далее применяют указанные выше формулы.