БСЭ - Большая Советская энциклопедия (Пр)

1) Определение u и j по измерениям z светила s . Из параллактического треугольника PZ s ( Р — полюс мира, Z — зенит, s — место светила; рис. 1 ) следует, что

cos z = sinj sind + cosj cosdcos t , (1)

где

t = Т + u — a. (2)

Найдя в астрономическом каталоге a и d наблюдаемого светила и измерив его зенитное расстояние z в момент Т, из уравнений (1) и (2) можно вычислить поправку часов u , если известна j, или вычислить j, если известна u. Если неизвестны u и j, то решение уравнений (1) и (2) ведут способом последовательных приближений или наблюдают две звезды: одну вблизи меридиана, другую — вблизи первого вертикала. Полученные две системы уравнений (1) и (2) решают совместно. Для моментов кульминаций справедливы уравнения:

j = d s+ Z s и j = d N— Z N (3)

(индексы S и N обозначают светила, кульминирующие, соответственно, к югу и северу от зенита). Т. к. измерить z строго в меридиане нельзя, то измеряют его вблизи меридиана, вводя при вычислениях необходимую поправку.

2) Определение u и j по наблюдениям пар звёзд на равных зенитных расстояниях z . В 1874 русский геодезист Н. Я. Цингер предложил способ определения u по наблюдениям моментов прохождения двух звёзд через один и тот же альмукантарат (см. Цингера способ ) . Звёзды наблюдаются вблизи первого вертикала: одна — на востоке, другая на западе, симметрично относительно меридиана. Аналогичный способ для определения j по наблюдениям пары звёзд на равных зенитных расстояниях вблизи меридиана предложил в 1887 русский путешественник М. В. Певцов (см. Певцова способ ) . Оба способа характеризуются простотой наблюдений и высокой точностью получаемых результатов.

3) Совместное определение u и j. Советские учёные В. В. Каврайский (1924—36) и А. В. Мазаев (1943—45) предложили способы совместного определения u и j (см. Каврайского способ и Мазаева способ ) . По способу Каврайского наблюдаются четыре звезды на попарно равных зенитных расстояниях z ; по способу Мазаева — серия звёзд в альмукантарате с z = 45° или z = 30°.

4) Определение j по способу Талькотта. Этот способ, предложенный в 1857 американским геодезистом А. Талькоттом, основан на измерении малой разности зенитных расстояний двух звёзд, кульминирующих по разные стороны от зенита (см. Талькотта способ ) . Полусумма правых и левых частей равенств (3) даёт:

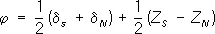. (4)

Звёзды выбираются так, чтобы разность их зенитных расстояний была в пределах диаметра рабочей части поля зрения трубы, т. е. не превышала 10—15’, а разность прямых восхождений отличалась бы на 5—20 мин (при наблюдениях обеих звёзд в верхней кульминации). Для наблюдений труба зенит-телескопа или универсального инструмента устанавливается на среднее зенитное расстояние пары в азимуте 0° для наблюдения звезды, кульминирующей к югу от зенита, и 180° — к северу от него. Величина Z s— Z N измеряется окулярным микрометром. Способ нашёл широкое применение, в частности на международных станциях, изучающих движение земных полюсов.

5) Определение u и j из наблюдений на зенитной фотографической трубе. В некоторых обсерваториях для служб времени и служб широты определяют u и j из совместных наблюдений на фотографических зенитных трубах. Изображение звезды фиксируется на движущейся с её скоростью фотографической пластинке с маркировкой на ней моментов времени. Звёзды наблюдают в узкой зенитной зоне, ограниченной рабочей частью поля зрения трубы. Ось инструмента постоянно направлена в зенит, что контролируется ртутным горизонтом.

6) Определение u пассажным инструментом. Этот способ широко применяется в практике служб времени и при высокоточных определениях долгот. Наблюдаются моменты прохождений серии звёзд через меридиан с регистрацией их или контактным микрометром, или с помощью фотоумножителей. Поправки определяются по формуле

u = a — Т. (5)

Подобный способ применительно к универсальному инструменту предложил русский геодезист Н. Д. Павлов (1912). В некоторых случаях определение u производится по наблюдению прохождений звёзд в вертикале Полярной (способ Деллена ) .

7) Определение l. Восточная долгота места наблюдения связана со всемирным временем S и местным s соотношением:

l = s — S = Т + u — S; (6)

u — определяется одним из изложенных выше способов, а S — путём приёма радиосигналов времени, транслируемых в течение суток многими радиостанциями.

8) Определение А. Наиболее распространённый способ основан на измерении универсальным инструментом горизонтального угла между направлениями на Полярную М s( рис. 2 ) и земной предмет М и вычислении азимута Полярной в момент наблюдения s. Для этого служит соотношение:

tga 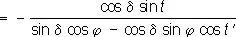, (7)

где t = s — a . Азимут А предмета находится из уравнения

А = а + М — М s. (8)

В геодезической практике часто применяется способ определения азимута, основанный на наблюдениях моментов прохождения звёзд с большими z (50°—70°) вблизи меридиана.

9) Определение j и l способом высотных линий положений, предложенным американским моряком Т. Сомнером в 1843 (см. Сомнера способ ) . В мореходной и авиационной астрономии, где требуется меньшая точность, но большая быстрота в определении j и l, широко применяется способ высотных линий положения, сущность которого ясна из рис. 3 . Находясь в точке m, географические координаты которой необходимо определить, измеряют зенитное расстояние z 1 небесного светила s 1(с координатами a 1и d 1) и вычисляют географические координаты проекции å 1, светила на поверхность Земли — т. н. географические места светила — по формулам j 1= d; l 1= a 1— S (долгота восточная). Окружность радиуса z 1 с центром в å 1проходит на глобусе через точку m. Измерив z 2 другого светила, проводят другую окружность радиусом z 2 с центром в å 2; в одной из двух точек пересечения этих окружностей расположена искомая точка m (выбор нужной точки не представляет затруднений, т.к. приближённое. место наблюдения бывает известно). На практике пользуются не глобусом, а картой, прочерчивая на ней отрезки кривых, отождествляемые с дугами окружности вблизи их пересечений. Эти отрезки называют высотными линиями положений или линиями Сомнера (см. Позиционная линия ) .